学習数学研究紀要　創刊号（第1巻）

カテゴリ： MMP
作成日： 2019/12/23 16:49:54
要約：学習数学研究所は、当協会における研究の基盤を担い、実用数学技能検定（数学検定・算数検定）を中心とした研究及び調査を行い、数学の生涯学習の進歩発展に寄与することを目的として、2016年2月に設置された研究機関です。

ページ： 1
学習数学研究紀要創刊号（第１巻）公益財団法人日本数学検定協会学習数学研究所
▲TOP

ページ： 2
学習数学研究所紀要目次巻頭言………………………………………………………………………………………… 清水静海 1 学習数学研究所紀要創刊に寄せて………………………………………………………… 一松信 2 学習数学研究所紀要創刊に寄せて………………………………………………………… 甘利俊一 3 学習数学研究所紀要創刊に寄せて………………………………………………………… 合原一幸 4 学習数学研究所設立の経緯………………………………………………………………………………… 5 【研究論文】新学習指導要領が目指すこれからの算数・数学科の教育…………………………… 清水静海 6 数学の科学・工学分野への適用調査…………………………………………………… 中村力「縮図や拡大図」地図上の実際の長さを求めるときに見られる誤答－算数検定６級の答案の分析を通して－…………………………………… 【研究ノート】三乗和の公式の簡単な求め方…………………………………………………………… 一松信数学カレンダーの作製は数学学習の普及を目指して………………………………… 渡辺信【報告】公益財団法人日本数学検定協会が「記述式」を重んじる理由……………………………………… 44 飯高先生の数学講座……………………………………………………………………………………… 46 文部科学省委託事業及び関連する事業－「高校生のための学びの基礎診断」（高等学校基礎学力テスト（仮称））－ …………… 47 数学検定の海外への普及………………………………………………………………………………… 48 学習支援…………………………………………………………………………………………………… 49 イベントの実施…………………………………………………………………………………………… 49 教員採用試験問題（数学）の分析……………………………………………………………………… 49 【会議報告】学習数学研究所運営会議議事録……………………………………………………………………… 50 検定問題品質会議………………………………………………………………………………………… 52 検定問題等検討会………………………………………………………………………………………… 53 【規程類】公益財団法人日本数学検定協会（学習数学研究所）公的研究費に係るルールの全体像………… 54 公益財団法人日本数学検定協会学習数学研究所規程……………………………………………… 55 組織図……………………………………………………………………………………………………… 58 公益財団法人日本数学検定協会学習数学研究所運営規程………………………………………… 59 研究者の行動規範………………………………………………………………………………………… 62 編集後記……………………………………………………………………………………………………… 65 【付録】実用数学調査（全体俯瞰マップ）１．力学系数学俯瞰チャート２．電気系数学俯瞰チャート３．情報系数学俯瞰チャート４．金融工学 / 経済学俯瞰チャート 40 42 松本精一 28 33 「3.1＋5.9」についての扱い…………………………………………………………… 渡辺信 23
▲TOP

ページ： 3
巻頭言学習数学研究所所長清水静海(*) 平成 11 年 7 月文部科学省の認可を受けて財団法人日本数学検定協会が発足しました。この法人の目的の一つに「学習数学の体系的研究を推進する」ことがあり、そのため、平成 13 年学習数学研究所を設立し、同年には文部科学省より科学研究費補助金取扱規程で定められた研究機関に指定されました。しかし、諸般の事情により平成 22 年 6 月学習数学研究所をやむを得ず閉じることとしました。平成 25 年 10 月、財団法人日本数学検定協会は財団法人から公益財団法人に法人格を移行し、「当協会における研究の基盤を担い、実用数学技能検定（数学検定・算数検定）を中心とする研究及び調査を行い、数学の生涯学習の進歩発展に寄与する」ことを目的として、平成 28 年 2 月学習数学研究所(以下、単に研究所とする。)を設立しました。研究所の主要な事業は、①数学の生涯学習に関する研究の実施、②検定に関する研究の実施、③算数教育及び数学教育に関する研究の実施、④研究会・講演会等の開催、⑤紀要の刊行等です。これらの事業には、研究所員はじめ、協会員ならびに研究所をお支えいただいています幼小中高大学の教員を中心に構成されたシンクタンクの皆様に深くかかわっていただき、多くの方々のご支援により展開されています。この度、公益に資する活動を展開する一貫として、研究所の研究や活動等について取りまとめ、紀要として公にし、情報を共有することとなりました。研究所設立後、平成 30 年 3 月までのおよそ 2 年間に、研究部門で実施した「数学の生涯学習」、「検定結果の分析」、「コンテンツの開発」に関する研究の内容を論文等記事にまとめるとともに、運営部門、検定問題品質管理部門の活動に関する内容も掲載することとしました。学習指導要領が改訂され、小学校では2020年度から、中学校では2021年度からそれぞれ完全実施され、高等学校では2022年から学年進行で実施されることになっています。育成を目指す資質・能力が「知識及び技能」、「思考力，判断力，表現力等」、「学びに向かう力，人間性等」の三つの柱に基づいて整理され、自立と協働による創造を支え、価値ある新たなものを生み出すものとして働くようにし、「人間ならではの強み」を明らかにし、それを活かすことを中核においた教育が実施されようとしています。算数や数学の学びを通して育まれた資質・能力は、こうした方向を基盤として支えることができると確信しています。紀要の創刊を機に、生涯学習及び算数・数学教育に関する研究活動をさらに進めて、将来に渡って有用な情報を発信し、社会に貢献できる体制を整えてまいります。また、当協会の一松信名誉会長、甘利俊一会長、合原一幸理事から紀要の創刊に寄せてお祝辞をいただきました。皆様からのご期待を今後の活動の励みとして精進してまいります。皆様からのご指導、ご鞭撻、引き続き宜しくお願いします。 (*)公益財団法人日本数学検定協会理事長・帝京大学教育学部教授－1－
▲TOP

ページ： 4
学習数学研究所紀要創刊に寄せて学習数学研究所特別顧問一松信(*) この度，学習数学研究所紀要を創刊することになりました。公益財団法人日本数学検定協会においては，以前から数学検定を実施するだけでなく，生涯学習の一環として，学習数学の体系的研究を重要な業務の一つと考えてきました。別掲の学習数学研究所設立の経緯にあります通り，かなり以前に（第１期）学習数学研究所を発足させました。そして文部科学省から，科学研究費補助金取扱規程で定められた研究機関に指定されました。しかし不幸なことに，諸般の事情により十分な活動を行うことができず，一旦研究所を廃止し，研究機関廃止届を提出する羽目に陥りました。その後内閣府の許可を受けて，現在の公益財団法人日本数学検定協会が発足し，改めて１年余りの準備の後，学習数学研究所の再開にこぎつけました。幸い文部科学省から学術研究機関としての指定を受けることができ，予定よりも遅れましたが，当研究所の紀要の刊行を果たすことになりました。研究所の諸規定や，当紀要の趣旨・投稿規定などは別掲の諸記事を御参照ください。これまでにもマスマスプラスなどのニュースレターを発行して，当協会の事業を紹介して参りましたが，今後定期的に本紀要を通じて，学習支援やイベントの紹介，さらには各種の研究論文の発表や事業報告などの広報活動に資するようにいたします。数学検定は単なる「試験」ではなく，生涯に渡る学習成果の達成度を計り，社会に役立つ「資格」であることを目標としております。今回の紀要創刊を一つの節目として，ますますの発展を念願するものです。創刊に当たり，今後の活動を期待する次第です。 (*)公益財団法人日本数学検定協会名誉会長・京都大学名誉教授－2－
▲TOP

ページ： 5
学習数学研究所紀要の創刊に寄せて学習数学研究所顧問甘利俊一(*) 世の中には数学好き、数学が好きで好きでたまらないという人が実は多い。数学が面白いからである。脳は数学が好きらしい。人類は進化の過程で素晴らしい脳を作り上げた。脳は必要な情報処理を素早く的確に行うだけではない。ここに意識を宿し、論理的推論を行う。人は社会生活を送る動物である。共同作業を行うには、自分のこれからすることを人に伝えなければならない。そのためには自分の意図を自分で知ることが必要である。ここから意識が生じた。さらに、人に伝えるために言語と論理を発展させた。数学の基礎は実はここにある。人は理詰めで考えることが好きである。考えの通りに物事が進めば快感を覚える。数や図形についての考えを抽象化すれば、数学に至る。数学は古代から、世界各地で文明の発生とともに誕生した。古代バビロニアでは、今から 4000 年も前にピタゴラスの定理（三平方の定理）に相当するものが知られており、その計算法が確立していたという。数学を、公理、証明、定理の整然とした体形にまとめたのはギリシャの数学である。ユークリッドの「原論」に見るように今から 2500 年も前の話である。私は「素数は無限個ある」という定理とその証明が好きだ。どうしてこんなことを考え、こんな証明に至ったのか、今から考えても素晴らしいではないか。時代は変わり近代科学が成立すると、数学は科学を理解し、記述するための欠かせない道具となった。さらにそれ自体が高度に発展し、抽象数学を生み出した。こうなると、専門の数学者にしか理解できない高嶺の学問となるのはやむを得ない。一方、学校教育で数学を教えるのは大変いいが、これが暗記物の苦行となれば、数学の楽しさなどどこかへ吹っ飛んでしまう。こうして学校教育は多数の数学嫌いを生みだしてしまった。何しろ、４人の子供に紙を３枚ずつ配るのに何枚必要かという問いに、３×４ならば正しくて４×３は誤りであるというような教え方が続いていた。最近になってやっと、どちらでもよいことにするという注が学習指導要領に付いたという。でも、数学好きは後を絶たない。面白いからだ。別に数学者に限る必要はない、科学者、技術者ではなくて、文科系でも数学好きは多数いる。数学嫌いを作ってはいけない。さらに数学好きに活躍の場を与えたい、こんな願いから日本数学検定協会が発足して 30 年になる。私たちは、数学好きの芽を育て、また多くの人に腕試しの場を与えたい。そのためには、組織だった活動が必要である。数学検定といっても、質の良い問題を作成するのは大変なことだ。実は恥ずかしながら私も昔，作成と検討に携わったことがあったが、もう年を取ってその任に堪えない。学習数学研究所は、数学検定にかかわる研究と調査を行い、さらに数学の生涯学習の進歩発展に寄与することを目的として、日本数学検定協会内に設立された。この度、研究所の紀要が創刊され、その素晴らしい活動が皆さんの目に触れる形で公開されることになった。大変喜ばしいことである。 (*)公益財団法人日本数学検定協会会長・東京大学名誉教授－3－
▲TOP

ページ： 6
学習数学研究所紀要創刊に寄せて学習数学研究所顧問合原一幸(*) 人類を他の生物と区別する最も重要な特徴のひとつは、その言語能力である。人類は、進化の過程で言語を生み出すことによって、高度なコミュニケーション能力や思考能力を獲得したと考えられている。そして、意識や心の発生とも、言語は深く関係しているように思われる。筆者からみると、数学は世界共通のとりわけ優れた“言語”である。ダイナミズムに満ちたこの動的世界の諸現象を記述するのに、差分方程式や微分方程式以上の記述能力を有する言語は他には思いつかない。たとえば、ロジスティック写像 x(t＋1) ＝ax(t)(1－x(t))（ただし、x(t)は実数値変数、t ＝ 0, 1, 2,..., a は [0,4] の実数値をとるパラメータ）は、様々なカオス解や周期解、周期解の周期に関するシャルコフスキーの順序、そしてカオス解の生成に至る周期倍分岐や接線分岐などの分岐構造を生み出す。これらの複雑さが、2 次関数の非線形性のみを持つこの簡単な１次元写像（差分方程式）で記述出来るというのは、実に驚くべきことである。そして、このロジスティック写像が生み出す複雑さの全貌を、自然言語で書き表すことは到底不可能である。言語に関わる人類のもうひとつの大きな発明は、文字である。音声言語自体は、その瞬間瞬間に消えてなくなるため、この点で言語の発生の進化的研究はきわめて難しい。これに対して、文字の発明によって、人類はその記憶を外在化して長時間もしくはほぼ永久的に残すことを可能にした。すなわち、文字によって、容易に時空の壁を越えることが出来たのである。今回の紀要創刊の意義は、ここにある。本学習数学研究所紀要の創刊によって今後、算数教育、数学教育、さらには数学の生涯学習等々に関する、本研究所での様々な知見が蓄積され広く活用されていくことになろう。心からお喜び申し上げる。 (*)公益財団法人日本数学検定協会理事・東京大学生産技術研究所教授－4－
▲TOP

ページ： 7
学習数学研究所設立の経緯平成 25 年（2013 年）財団法人日本数学検定協会は、内閣府の認可を受けて財団法人から公益財団法人に法人格を移行した。平成 27 年（2015 年）10 月 1 日学習数学研究所開設準備室を設立した。平成 28 年（2016 年）2 月 1 日学習数学研究所を開設した。(*) 目的：当協会における研究の基盤を担い、実用数学技能検定（数学検定・算数検定）を中心とする研究及び調査を行い、数学の生涯学習の進歩発展に寄与すること平成 29 年（2017 年）8 月 31 日文部科学省から学術研究機関としての指定を受けた。研究所の事業 ①数学の生涯学習に関する研究 ②検定に関する研究 ③算数教育及び数学教育に関する研究 ④研究会・講演会等の開催 ⑤紀要の刊行 ⑥その他 (*)平成 11 年（1999 年）7 月 13 日文部科学省の認可を受けて、財団法人日本数学検定協会が発足した。平成 13 年（2001 年）協会内に、学習数学の体系的研究を推進するため学習数学研究所を設立した。平成 13 年（2001 年）12 月 21 日学習数学研究所は、文部科学省より、科学研究費補助金取扱規程で定められた研究機関に指定されたが、平成 22 年（2010 年）6 月 21 日諸般の事情により廃止することとなった。－5－
▲TOP

ページ： 8
【研究論文】
▲TOP

ページ： 9
平成 30 年 3 月新学習指導要領が目指すこれからの算数・数学科の教育 (*) 学習数学研究所清水静海要約平成期の 30 年間に小中学校学習指導要領は４回改訂され(平成元、10、20、29 年)、成熟社会における教育の在り方について模索が続けられてきた。平成 29 年改訂の学習指導要領において、その完成形に近いものが示され、実現を目指す教育の全貌が一層的確かつ精緻に記述されたとみることができる。本稿では、小中学校算数・数学科の教育に視点を当て、平成 20 年改訂と平成 29 年改訂小中学校学習指導要領を対比しながら、後者の特徴を顕在化することを主たる目的とする。このため、①教育目標の教育内容への反映、②〔算数的活動〕と〔数学的活動〕の位置づけにおける｢ねじれ｣の解消、及び③プログラミング教育の導入に焦点を当て、 ①については相互の関連性が明確にされたこと、②については｢ねじれ｣が解消され教育内容としての位置付けが明確になったこと、③については中長期的な視野に立ち冷静な対応が必要であることをそれぞれ明らかにした。キーワード：学習指導要領、数学的活動、プログラミング教育はじめに小中学校の学習指導要領(告示：以下｢次期｣とする([1])。)が平成 29 年 3 月 31 日公示され、平成 32 年度小学校、同 33 年度中学校の全面実施に向け、｢次期｣が実現を目指す教育を確かに、そして豊かに展開していくことが期待されている。ここでは、小中学校の算数･数学科(以下、小中学校の算数･数学科、小学校算数科、中学校数学科を、それぞれ算数･数学科、算数科、数学科とする。)に視点をおいて、｢次期｣の特徴を整理し、併せて理論的研究、実践的研究への期待を述べる。中央教育審議会(以下、中教審とする。)教育課程部会教育課程企画特別部会で小中高校の算数・数学科の改善の基本的方向や見直しの視点が整理され([2])、答申([3])を踏まえて｢次期｣は作成された。改善の基本的方向では｢算数・数学を学習する楽しさや学習する意義の実感｣と｢数学のよさの認識｣が強調され、見直しの視点としては、｢育成すべき資質・能力の明確化｣と｢算数的活動・数学的活動の充実｣、「統計的な内容等の改善」(以上、小・中・高共通)及び｢選択－6－
▲TOP

ページ： 10
科目『数理探究』(仮称）の設置の検討」(高)の三つが挙げられた([2])。ここでは、前二者に焦点をあて、教育目標の構造化及びその背景、数学的活動の充実に視点をおいて検討する。１．算数・数学科の教育目標の構造化と教育内容第二次世界大戦後、昭和 30 年代以降の告示｢学習指導要領｣では、算数・数学科の教科目標は、教科全体を総括する目標(教科目標)と各学年の目標(ここでは、以上を教育目標とする。)で構成され、その趣旨が教育内容の構成、特に各指導事項([4])の記述に反映されてきた。｢次期｣では、教育目標の示し方の大枠は平成 20 年改訂の現行学習指導要領(以下｢現行｣とする。)までと同様であるが、その内容が一層精緻化され相互の関連の｢見える化｣が図られている。｢次期｣では 50％程度文言が増えているといわれるが、ざっくり言えば、これまで行間に埋め込まれていたことが顕在化され、構造的に一層分かりやすく示されたと見てよい。ここでは、算数・数学科の教育目標の構造化とその教育内容の記述への反映、及びそれらの背景にあることに着目し、教育目標と教育内容の一体化が図られ、一定の評価ができることを明らかにする。 (1) 教科目標の二重構造化｢次期｣の教科目標は総括的な目標と具体的な目標の二重構造で示され(昭和 43、44 年の改訂と同様、学習指導要領解説(算数、数学)では、それぞれ、柱書、柱としている。)、算数・数学科の教育の要点は、総括的な目標｢数学的な見方・考え方を働かせ，数学的活動を通して，数学的に考える資質・能力を次のとおり育成することを目指す｣(小中共通)で端的にまとめられ、高等学校数学科の教科目標にも反映される予定である。この総括的な目標は、｢数学的に考える資質・能力を育成すること｣を中核とし、｢数学的活動｣と｢数学的な見方・考え方｣で包む構造で整理されている。なお、｢数学的に考える資質・能力｣は、平成 16 年度に実施された｢特定の課題に関する調査｣において｢数学的活動を遂行するために必要な資質や能力の総称｣と定義された｢数学的に考える力｣とほぼ同義であり、この定義における｢資質｣を｢次期｣の枠組みに合わせて表に出し｢数学的に考える資質・能力｣としたものといえる。これを受け、具体的な目標は、育成を目指すべき資質・能力の３本の柱、｢生きて働く知識・技能(以下、｢知識･技能｣とする。)の習得｣、｢未知の状況にも対応できる思考力・判断力・表現力等(以下、｢能力｣とする。 )の育成｣、及び｢学びを人生や社会に生かそうとする学びに向かう力・人間性(以下。｢態度｣とする。)の涵養｣に対応させ、学校段階や各学年に配慮して構成され、記述されている(下線引用者)。算数･数学科の教科目標は次のようである(下線引用者)。算数科総括的な目標数学科数学的な見方・考え方を働かせ，数学的活動を通して，数学的に考える資質・能力を次のとおり育成することを目指す。 (1)知識･技能数量や図形などについての基礎的・基本的な概念や性質などを理解するとともに，日常の事象を数理的数量や図形などについての基礎的な概念や原理・法則などを理解するとともに，事象を数学化したり，数学的に解－7－
▲TOP

ページ： 11
に処理する技能を身に付けるようにする。具体的な目標 (2) 能力日常の事象を数理的に捉え見通しをもち筋道を立てて考察する力，基礎的・基本的な数量や図形の性質などを見いだし統合的・発展的に考察する力，数学的な表現を用いて事象を簡潔・明瞭・的確に表したり目的に応じて柔軟に表したりする力を養う。 (3) 態度数学的活動の楽しさや数学のよさに気付き，学習を振り返ってよりよく問題解決しようとする態度，算数で学んだことを生活や学習に活用しようとする態度を養う。釈したり，数学的に表現・処理したりする技能を身に付けるようにする。数学を活用して事象を論理的に考察する力，数量や図形などの性質を見いだし統合的・発展的に考察する力，数学的な表現を用いて事象を簡潔・明瞭・的確に表現する力を養う。数学的活動の楽しさや数学のよさを実感して粘り強く考え，数学を生活や学習に生かそうとする態度，問題解決の過程を振り返って評価・改善しようとする態度を養う。｢知識･技能｣では、技能にかかわって｢事象を数学化したり，数学的に解釈したり｣する技能が例示されていることが特徴的である。つまり、数学的活動、すなわち数学的探究(問題発見・解決)を遂行する上で必要となる方法に着目した技能及びそれを支える知識を身に付けることの必要性を強調したものと言える。｢能力｣では、｢考察する力｣と｢表現する力｣で括られている。なぜ、｢考える｣ではなくて｢考察｣なのか、考察の意味について、また、表現の意義や働きなどについてそれぞれ検討が必要になろう。｢態度｣では、問題解決の文脈での PDCA サイクルや学んだことを生活や次の学習に生かす視点で学びに向かう力を支える態度が例示され、それらを強化する要素として｢数学的活動の楽しさ｣と｢数学のよさ｣への気付きやそれらの実感を明確に位置づけている。なお、育成すべき資質･能力の三つの要素、｢知識及び技能｣、｢思考力、判断力、表現力等｣、｢学びに向かう力、人間性等｣には、観点別学習状況の評価の観点の｢知識・技能｣、｢思考･判断・表現｣、｢主体的に学びに向かう態度｣(人間性等は評定になじまないので、個人内評価で対応する。したがって、この観点では学びに向かう力が評価の対象となる。)がそれぞれに対応することが明らかにされている。 (2) 各学年の目標の再構成と教育内容との関連性の明確化各学年の目標は、これまで｢現行｣までは各領域のまとまりごとに、発達段階に配慮し、教科目標の要点を反映させ、知識･理解と能力に視点をおいて整理してきていた。｢次期｣では、それを、上述の教科目標の具体的な目標の３本柱に対応させて記述する構造に改め、教科目標と各学年の目標との関連性を一層明確にしている。たとえば、中学校第一学年数学科の目標について対比すると次のようである(下線引用者)。－8－
▲TOP

ページ： 12
現行（平成 20 年改訂） (1) 数を正の数と負の数まで拡張し，数の概念についての理解を深める。また，文字を用いることや方程式の必要性と意味を理解するとともに，数量の関係や法則などを一般的にかつ簡潔に表現して処理したり，一元一次方程式を用いたりする能力を培う。〔Ａ数と式〕次期（平成 29 年改訂） (1) 正の数と負の数，文字を用いた式と一元一次方程式，平面図形と空間図形，比例と反比例，データの分布と確率などについての基礎的な概念や原理・法則などを理解するとともに，事象を数理的に捉えたり，数学的に解釈したり，数学的に表現・処理したりする技能を身に付けるようにする。〔(1) 知識・理解〕 (2) 数の範囲を拡張し，数の性質や計算について考察 (2) 平面図形や空間図形についての観察，したり，文字を用いて数量の関係や法則などを考察し操作や実験などの活動を通して，図形に対する直観的な見方や考え方を深めるとともに，論理的に考察し表現する能力を培う。〔Ｂ図形〕たりする力，図形の構成要素や構成の仕方に着目し，図形の性質や関係を直観的に捉え論理的に考察する力，数量の変化や対応に着目して関数関係を見いだし，その特徴を表，式，グラフなどで考察する力，デ (3) 具体的な事象を調べることを通して，ータの分布に着目し，その傾向を読み取り批判的に考比例，反比例についての理解を深めるとともに，関数関係を見いだし表現し考察する能力を培う。〔Ｃ関数〕察して判断したり，不確定な事象の起こりやすさについて考察したりする力を養う。〔(2) 能力〕 (3) 数学的活動の楽しさや数学のよさに気付いて粘り強く考え，数学を生活や学習に生かそうとする態 (4) 目的に応じて資料を収集して整理し，度，問題解決の過程を振り返って検討しようとする態その資料の傾向を読み取る能力を培う。〔Ｄ資料の活用〕度，多面的に捉え考えようとする態度を養う。〔(3) 態度〕｢現行｣では、それまで同様、学年目標を内容領域に対応させて整理しているが、それに伴い、各項目には理解や技能にかかわる要素に能力にかかわる要素が組み込まれる形式で位置づけられている。｢次期｣では、それを｢知識・理解｣及び｢能力｣で括り、さらに｢態度｣を加えて三つの柱で系統が明確になり、一層精緻化されて整理されている。さらに、｢次期｣では教育目標(教科目標及び学年目標)と指導事項との関連も構造的に整理し、一層明確にしている。たとえば、｢現行｣の算数科第一学年領域｢Ａ数と計算｣の指導事項(2)で見てみよう。次頁のようである(下線引用者)。｢現行｣は｢(2)加法及び減法の意味について理解し、それらを用いることができるようにする｣を受け、｢ア加法及び減法が用いられる場合について知ること｣などと指導項目を示す形式で、現行（平成 20 年改訂）次期（平成 29 年改訂） (2) 加法及び減法に関わる数学的活動を通して，次の事項を身に付けることができるよう指導する。ア次のような知識及び技能を身に付けること。 (2) 加法及び減法の意味について (ｱ) 加法及び減法の意味について理解し，それらが用いら－9－
▲TOP

ページ： 13
理解し，それらを用いることができるようにする。ア加法及び減法が用いられる場合について知ること。イ１位数と１位数との加法及びその逆の減法の計算の仕方を考え，それらの計算が確実にできること。ウ簡単な場合について，２位数などの加法及び減法の計算の仕方を考えること。れる場合について知ること。 (ｲ) 加法及び減法が用いられる場面を式に表したり，式を読み取ったりすること。 (ｳ) １位数と１位数の加法及びその逆の減法の計算が確実にできること。 (ｴ) 簡単な場合について，２位数などについても加法及び減法ができることを知ること。イ次のような思考力，判断力，表現力等を身に付けること。 (ｱ) 数量の関係に着目し，計算の意味や計算の仕方を考えたり，日常生活に生かしたりすること。｢現行｣では、知識や技能にかかわることと能力にかかわることが、学年目標の場合と同様に混在している。｢次期｣では、｢現行｣の(2)が｢ア次のような知識及び技能を身に付けること｣と｢イ次のような思考力，判断力，表現力等を身に付けること｣として｢知識・技能｣と｢能力｣に対応する項目に分割され、それぞれの下位項目として｢(ｱ)加法及び減法の意味について理解し、それらが用いられる場合について知ること｣や｢(ｱ)数量の関係に着目し、計算の意味や計算の仕方を考えたり、日常生活に生かしたりすること｣として位置づけられている。そして、アとイを総括する形で、教科目標の総括的な目標の趣旨を反映し、｢(2)加法及び減法に関わる数学的活動を通して，次の事項を身に付けることができるよう指導する｣を新設し、各指導事項の指導では｢数学的活動を通して｣行うことを明示している。結果、｢能力｣に関わる内容が顕在化されることとなった。なお、｢態度｣に対応する項目の記述は各指導事項に明示されていないが、それは学年目標の(3) で代表させ、それぞれの指導事項の指導の前提としており、重複を避けていると見てよい。 (3) 教育目標等の構造化の背景にあること今世紀は｢新しい知識・情報・技術が、社会のあらゆる領域での活動の基盤として飛躍的に重要性を増していく｣知識基盤社会と言われて久しい。最近、「進化した人工知能が様々な判断を行ったり、身近な物の働きがインターネット経由で最適化されたりする時代」の到来、いわゆる第４次産業革命の進展が言われている。｢次期｣での教育目標等の構造化の背景にはこれらの社会の変化への認識があったと見てよい。現在進行中の第四次産業革命のまっただ中で、たくましく、そして豊かに生き抜いてけるために、児童･生徒が学校教育を通じて身に付ける必要がある資質・能力をどのようにとらえたらよいか、そして、それらをどのように身に付けていくか、いずれも｢次期｣での重要な論点であり、今後も引き続き重要な論点となるであろう。こうした背景の中で、｢次期｣では、｢人間ならではの強み｣に着目し、生きる力の再構造化を図ることでこのことに対応しようとしていると言える。ここでは、そのことに視点をおいて、ポイントを整理することとする。 ① 人間ならではの強みの意識人間ならではの強みを｢感性を豊かに働かせながら、どのような未来を創っていくのか、どの－10－
▲TOP

ページ： 14
ように社会や人生をよりよいものにしていくのかという目的を自ら考え出すことができる｣ ([4])として、｢解き方があらかじめ定まった問題を効率的に解いたり定められた手続を効率的にこなしたりすること｣にとどまらず、｢主体的に学び続けて自ら能力を引き出し、自分なりに試行錯誤したり、多様な他者と協働したりして、新たな価値を生み出していくために必要な力を身に付け｣ことや｢予測できない変化に受け身で対処するのではなく、主体的に向き合って関わり合い、その過程を通して、自らの可能性を発揮し、よりよい社会と幸福な人生の創り手となっていけるようにする｣ことが重要であるとしている。今年 1 月、ある業界新聞の新春座談会([5])で、人工知能関連の仕事に携わっている方々と意見交換する機会があった。印象に残ったことは、｢０から１を創り出すことの重要性｣の指摘とその過程で｢試行錯誤や試行接近を実体験することの大切さ｣についての指摘であった。いずれも、著名な数学者 G.ポリヤ(Polya：1887-1985)は、およそ 70 年前に探究の方法としての｢帰納｣を提案している([6])が、そこでの暗示的接触に関わることである。つまり、試行錯誤、試行接近、当て推量を経て推測の構成に至る過程である。彼は、推測の構成から始まり、思考実験(擬実験)、検証に至る過程を支持的接触とし、暗示的接触と合わせて帰納的手続きとしている。この手続きを支える態度として帰納的態度を挙げ、｢帰納｣はこれらをいわば車の両輪として展開するとするとしている。帰納的態度を構成する要素として、知的勇気、知的正直さ及び賢明なる自制を例示している。｢帰納｣は、今日育成を目指している資質・能力を身に付ける指導の急所を的確に示していると言える。実は、平成元年改訂の算数科([7])で｢問題解決｣を強調し｢思考実験｣を明示した背景にはこのことがあり、G.ポリヤ同様、数学教育の人間化を強く意識した対応であった。彼の主張の今日的な意義を明らかにし、算数･数学科の教育の進展に活かしていきたい。 ② ｢生きる力｣の再構造化｢次期｣では、平成 8 年に中教審で提案され、それ以来、知育の中核として、育成を目指してきている｢生きる力｣を一層精緻化し、各教科等の目標や内容の構成に反映している。中教審への諮問理由の説明([8])では、｢高い志や意欲を持つ自立した人間として、他者と協働しながら価値の創造に挑み、未来を切り開いていく力」(下線引用者)の育成を中核においた教育課程の基準等の改善を目指すことが明示され、｢現行｣における習得･活用･探究(習得と探究を活用でつなぐ)を発展させ、さらに、その上に｢自立と協働による創造｣にまで高める方向が示されている。これを受けて、答申([3])では「学校教育を通じて子供たちに育てたい姿」として｢自立と協働による創造｣の様相が再構成されている。まず、自立では｢主体的に学びに向かい、 (中略)、自ら知識を深めて個性や能力を伸ばし、人生を切り拓ひらいていくこと｣が、次いで、協働では｢他者の考えを理解し、自分の考えを広げ深めたり、集団としての考えを発展させたりすること｣が、最後に、創造では｢試行錯誤しながら問題を発見・解決し、新たな価値を創造していくこと｣がそれぞれ強調されている。これらは、｢『生きる力』を、現在とこれからの社会の変化の文脈の中で改めて捉え直し｣たもので、｢教育課程を通じて確実に育むことが求められている｣こととしている。－11－
▲TOP

ページ： 15
外山滋比古は、｢失敗経験が、成功の道を教えてくれる、失敗を知らずに成功をすることはまず不可能である｣、｢試行錯誤と言うが失敗の価値はきわめて大きい｣とし、｢汚れた泥の中から蓮は美しい花を咲かせるのである｣としている。育成を目指す資質・能力を育むために配慮したい大切なところを指摘している([9])。 ④ 世界をリードし、世界の子供たちの学びを後押しする「日本の改革は、もはや諸外国へのキャッチアップではなく、世界をリードする役割を期待されている。」とし、｢日本の子供たちの学びを支えるとともに、世界の子供たちの学びを後押しするものとすることが、今回の改訂に課せられた使命である。｣として、今回の改訂は世界を視野に入れたものとなっている([2])。今回の改訂の大枠については、平成 28 年 5 月倉敷市で開催された、G7 教育相会議の成果を取りまとめた倉敷宣言([10]、以下、倉敷宣言とする。)に見ることができる。｢Ⅰ．教育の果たすべき新たな役割(The New Role of Education)｣において次のように述べ、人間ならではの強みに着目し、それを強化することへの意識改革を求めている。予測困難な変化の激しい世界を生きる次世代が、自らが将来を作り出すことができるようにすべきとの認識のもと、与えられた課題に効率的に回答(ママ)する力にとどまらず、自ら新たな問いを立ててその解決を目指し、他者と協働しながら新たな価値を生み出していくための力を身に付けていく必要があることを我々は認識する。そして、次のように述べ、育成を目指す資質・能力の三つの柱が示されている。我々は、新たな時代に求められる児童生徒の資質・能力を育成していくためには、各国の実践や客観的根拠、またそれぞれ異なる国の様々な文化的、社会的、哲学的な背景を考慮しながら、全ての教育関係者が、例えば以下のような視点を教育実践の基盤として共有することが基本的な目標と考える。・What to know (acquiring knowledge) 何を知っているか・How to use knowledge (acquiring competencies ) 知っていることをどう使うか・How to engage in society and live a better life どのように社会・世界と関わり、よりよい人生を送るかさらに、次のように述べ、汎用的な資質・能力の育成と深い学びの実現を求めている。これらの視点に基づいた教育を実践することにより、子供達は、変化の激しいこれからの時代に求められる、コミュニケーションやコラボレーションのための能力、創造性、批判的思考、問題解決力、困難から立ち直る力等を含む)あらゆる汎用的な資質・能力を身につけ、市民社会や世界に関わっていくことができるようになると確信する。こうした能力は、しっかりとした教科の基礎的な知識とその知識の背景にある概念についての深い理解のもとに開発されるべきである。２．数学的活動の充実｢次期｣における算数・数学科の要点は数学的活動と統計的内容の充実であり([11])、ここでは、数学的活動の充実に焦点を当て、統計的内容の充実も視野に入れて検討する。そして、従前の改訂で課題とされた、〔算数的活動〕と〔数学的活動〕の位置づけにおける「ずれの解消」－12－
▲TOP

ページ： 16
ができたことは高く評価できること、統計的な内容における数学的活動には課題が残されていることを明らかにする。 (1) 数学的活動 ① 用語｢算数的活動｣、｢数学的活動｣の登場用語｢算数的活動｣、｢数学的活動｣が教育行政の文脈で初めて登場するのは、｢生きる力｣の育成が中核にすえられ、｢ゆとりの中で生きる力をはぐくむ｣ことを目指して改訂された平成 10 年の学習指導要領([12])の算数・数学科の教科目標においてである。算数科では、｢算数的活動を通｣して目標を実現する文脈と｢算数的活動の楽しさ｣に気付く文脈で位置づけられている。数学科でも同じ文脈で位置づけられ、この枠組みは基本的に｢現行｣に継承されている。この改訂の前提となった中教審答申の概要が英訳されており([13])、｢生きる力｣は ‘zest for living’([14])で、｢生きることへの渇望｣とされた([15])。また、｢ゆとり｣は‘room to grow’ で、｢成長にはすき間(あるいは、あそび)が必要であること｣を象徴する意味合いで訳された。今後の数学的活動の充実を巡る議論でも留意したいことである。 ② ｢現行｣での位置づけと改善｢現行｣では、教科目標での位置づけ(方法と目標)に、〔算数的活動〕や〔数学的活動〕として教育内容としての位置づけが加わった。しかし、両者では内容の例示の仕方に｢ねじれ｣があり、その調整は｢次期｣に残された。｢次期｣では、この｢ねじれ｣は解消され、〔算数的活動〕と〔数学的活動〕におけるリード文の末尾は次の表のようで、例示の仕方も統一され、教育の内容にふさわしい位置づけとなった(下線引用者)。現行（平成 20 年改訂）算数数学次のような算数的活動を通して指導するものとする。次のような数学的活動に取り組む機会を設けるものとする。次期（平成 29 年改訂）次のような数学的活動に取り組むものとする。次のような数学的活動に取り組むものとする。また、総括的な定義づけが共通の構造で精緻化された。すなわち、算数的活動は｢児童が目的意識をもって主体的に取り組む算数にかかわりのある様々な活動｣(以下、｢総括的定義｣とする。数学的活動では、算数を数学、活動を営みに置き換えていく。)とされ、児童と算数をそれぞれ生徒と数学に置き換えれば数学的活動の定義となる構造となっている([16])が、｢次期｣では、この定義を受け、｢答申｣ ([3]) の別添資料 4-2 ｢算数･数学の学習過程のイメージ｣に基づき、数学的活動の総括的定義を｢事象を数理的に捉え、数学の問題を見いだし、問題を自立－13－
▲TOP

ページ： 17
的、協働的に解決すること｣として、問題発見･問題解決の視点から分析的に整理し、その典型として日常生活や社会の事象からのものと、数学の事象からのものの二つを例示している。これを基に、｢次期｣における算数科の〔数学的活動〕の例示は｢現行｣の数学科の例示とそろえ ([17])、発達段階に配慮して典型的な活動を抽出して示しており、算数科と数学科の接続が滑らかになっている。ところで、｢総括的定義｣(H20 改訂時)の要点は、｢目的意識をもって主体的に取り組む｣ことと｢数学にかかわりのある｣ことである。前者は、｢次期｣における｢自立的、協働的な問題発見とその解決に主体的に取り組むこ｣とに、後者は｢主体的・対話的で深い学びの実現における深い学び｣にそれぞれ連なるものと言える。もちろん、数学に関わることは、単なる知識や技能、いわゆる事実知にとどまらない。それらを創る数学的探究の過程で必要な知識や技能、いわゆる方法知、それを遂行するために必要な諸能力、数学的探究を促し粘り強い遂行を支える意志や態度など、育成を目指す資質・能力に関わることの全体に及ぶものと捉えるべきである。 (2) 学習指導要領上の数学的活動の位置づけ ① 算数的活動と数学的活動の数学的活動による統合とその三つの側面｢次期｣では算数的活動は数学的活動に統合され、小中高で共通に数学的活動を用いることとなっている。それは、算数的活動も先人の英知の結晶としての数学を素材として展開しているからであり、ほぼ同趣旨で、これまでも算数科では、教科目標を構成する要素や観点別学習状況の評価の観点として｢算数的な考え方｣ではなくて｢数学的な考え方｣が用いられてきた。また、｢現行｣の英訳(仮訳)において、いずれも‘mathematical activities’とされていることなどによると思われる([13])。ところで、｢現行｣の解説数学編では、次のように述べ、数学的活動には三つの側面があることを既に明示している([17]、下線引用者)。数学的活動は，数学を学ぶための方法であるとともに，数学的活動をすること自体を学ぶという意味で内容でもある。また，その後の学習や日常生活などにおいて，数学的活動を生かすことができるようにすることを目指しているという意味で，数学的活動は数学を学ぶ目的でもある。つまり、数学的活動は教育の方法、内容及び目標の三つの側面をもつとしている。このことが、｢次期｣では学習指導要領解説算数編、数学編で一貫し、一層明確に示されることとなった。 ② 教育の方法としての位置づけ上述のように、｢数学的活動を通して｣との文言が教科目標の総括目標及び各学年・各領域の指導事項のリード文に明示され、算数科では｢第３指導計画の作成と内容の取扱い｣の３の冒頭で｢数学的活動は、基礎的・基本的な知識及び技能を確実に身に付けたり、思考力、判断力、表現力等を高めたり、算数を学ぶことの楽しさや意義を実感したりするために、重要な役割を果たす｣とし、教育の方法としての役割を総括している。 ③ 教育の内容としての位置づけ｢次期｣での数学的活動の教育の内容としての位置づけの記述では、上述のように、｢現行｣に－14－
▲TOP

ページ： 18
おける｢ねじれ｣が解消され、格段に改善されている。この位置づけの趣旨は、児童・生徒が自立的、協働的に問題発見とその解決に取り組むことを意図的、計画的に位置づけることが期待されており、教師にとっては日頃の学習指導の成果を評価し、改善する機会として重要になる。したがって、教育の方法として数学的活動を活かす過程では、児童・生徒が数学的活動に取り組むことができるために必要なこと整理し、意図的、計画的に指導することが一層重要になる。｢現行｣解説数学編([17])では、事例ごとに｢生徒が数学的活動に主体的に取り組むことができるよう、その前提となる指導についても触れる。｣として、生徒が数学的活動に取り組めるようにするための必要事項を例示している。なお、｢次期｣では、数学的活動の例示において、就学前の経験や小・中との接続、小学校６年間の発達段階への配慮などがより的確になされており、授業改善に活かしたい。 ④ 教育の目標としての位置づけ数学的活動の教育の目標としての位置づけは、たとえば、教科目標の具体的な目標や学年目標に反映しているとみてよい。すなわち、目標は教師を主語として記述されているが、たとえば、算数科の具体的な目標の(2)における｢数理的に捉え見通しをもち筋道を立てて考察する｣ことや｢性質などを見いだし統合的・発展的に考察する｣ことは、いずれも、教師が児童生徒を導き、できるようにする文脈で記述されている。それらは、いずれも数学に関わる営みであり、児童生徒がそれらに主体的に取り組めば、数学的活動の｢総括的定義｣に合致するし、この目標では、それらのことを児童生徒において確かにしかも豊かに実現することが期待されている。－15－
▲TOP

ページ： 19
⑤ 数学的活動を充実するための授業改善数学的活動を充実するための授業改善では、とりわけ、数学的活動の教育の方法及び内容としての側面が重要であると考える。すなわち、教育の目標としての数学的活動が児童・生徒において確かで豊かに実現できるよう導くことが重要だからである。このため、まず、単元全体または小単元全体を視野に入れた指導計画を立案することが大切である。数学的活動を通した意図的・計画的な指導と児童･生徒が数学的活動を実体験することのバランスをとることである。次いで、数学的探究の方法について、意図的、計画的な指導をすることが大切である。たとえば、授業の終末での学習のまとめでは、事実知にとどまらず方法知や学びに向かう力に関わることも対等に位置づけ児童の意識にしっかりと刻むことが必要となろう。その際、｢答申｣ ([3])の別添資料 4-3｢算数･数学の問題発見･解決のプロセスと育成すべき資質・能力｣が参考にできよう。 (3) 統計的な探究と数学的活動統計的な内容の充実については、｢社会生活などの様々な場面において、必要なデータを収集して分析し、その傾向を踏まえて課題を解決したり意思決定をしたりすることが求められており、そのような能力を育成するため、高等学校情報科等との関連も図りつつ、小・中・高等学校教育を通じて統計的な内容等の改善について検討していくことが必要である。｣([3])とされ、このことを受けて、領域｢Ｄデータの活用｣の新設と統計的な探究(問題解決や意志決定)の過程を重視することに視点をおいて充実を図っている。 ① 領域｢Ｄデータの活用｣の新設算数･数学科では、新領域｢Ｄデータの活用｣を設定し、内容の系統、各学年、各学校段階での指導の重点を一層明確にしている([18])。算数･数学科での統計的な内容は、昭和 30 年代の改訂で新設された領域｢数量関係｣の内容の一部分として位置づけられていたが、｢現行｣で、算数科では従前の第 3 学年からの｢数量関係｣を第 1 学年からに拡げ、数学科では領域｢数量関係｣を｢関数｣と｢資料の活用｣の二つの領域に分割し、一層の充実を図る方向で改訂さ－16－
▲TOP

ページ： 20
れた。｢次期｣では、上述のように、統計的な内容を算数･数学科で同一の領域名称｢Ｄデータの活用｣で括り、さらに充実させることとなった。これに伴い、算数科の領域は数学科の領域との関連に配慮して再編成されている。｢現行｣の｢Ｄ数量関係｣(式表現、関数的内容、統計的内容)の統計的な内容が｢Ｄデータの活用｣で括られたことにより、式表現(□や△、ｘ、ｙなど文字)は数学科の｢Ａ数と式｣との関連で｢Ａ数と計算｣へ、関数的内容は数学科の｢Ｃ関数｣との関連で新領域｢Ｃ変化と関係｣(第４学年～６学年)へそれぞれ移行している。さらに、算数科では図形についての考察が｢Ｂ量と測定｣と｢Ｃ図形｣の二つの領域に分けて示されてきたが、数学科の場合と同様に、｢Ｂ量と測定｣で取り上げていた面積や体積など図形の定量的把握についての内容を｢Ｃ図形｣の内容(図形の定性的把握についての内容)と統合し｢Ｂ図形｣としている。これにともない、従前の｢Ｂ量と測定｣で主として下学年で取り上げていた量の測定に関する内容をまとめて領域｢Ｃ測定｣を新設している。小･中学校の領域の再構成にともない、各領域の位置づけや趣旨に若干の変更があり、それらを内容の系統の整理、指導計画の作成、授業の改善にどのように反映させていくかなどが課題となっている。 ② 統計的な探究過程の重視｢小・中・高等学校を通じた統計教育のイメージ、内容等の整理(資料８)｣([19])において、たとえば、中学校数学では｢統計的に分析するための知識・技能を理解し、日常生活や社会生活の場面において問題を発見し、調査を行いデータを集めて表やグラフに表し、統計量を求めることで、分布の傾向を把握したり、二つ以上の集団を比較したりして、問題解決や意思決定につなげる｣こと及び｢データの収集方法や統計的な分析結果などを多面的に吟味する｣ことが例示されている([20])。これらのことは、右の図に整理して提案されている([21])。この図は、上述の｢算数･数学科の問題発見･解決の過程｣を統計的な探究の過程に援用したもので、とりわけ、｢データを収集しグラフにし分析すること｣を｢繰り返すこと｣及び｢多面的、批判的に考察すること｣を重視し、強調していることが特徴的である。これを受けて、小中学校学習指導要領解説(算数編、数学編)では、「問題(Problem)－計画 (Plan)－データ(Data)－分析(Analysis)－結論(Conclusion)」（PPDAC）と「データの収集・分－17－
▲TOP

ページ： 21
析を繰り返して、物事の判断をする」プロセスを重視することとして示されている([22])。 ③ 統計教育で期待されていること ― 情報活用能力の育成 ― 上述の倉敷宣言では、｢Ⅱ.教えや学びの改善・向上策｣を取りまとめた中で、二つの必要性、すなわち、「技術革新の悪用の可能性や様々な性質のオンライン情報の氾濫にも対処するため、我々は、子供や若者が情報の質や情報源を見分けるために必要なメディアや情報に関する能力を身に付けさせる必要性」と｢若者に影響力が大きいソーシャルメディアに関して、オンラインでの健全な社会的交流を行い、虚偽の情報と現実を区別し、事実と単なる意見をしっかり見極めることができるようになるための教育や指導｣の必要性への認識があった(下線引用者)。いずれも、情報の賢い受信者の育成を視野に入れている。もちろん、情報の発信者としてのモラルの育成にも通底する視野とも言える。すなわち、元号が昭和から平成に変わる頃、社会の情報化の進展を視野に入れ、それまでの用語｢情報処理能力｣は当時の臨時教育審議会(内閣直属)により、情報の創造と情報モラルの視点を加えた｢情報活用能力｣に発展的解消されることとなった。したがって、今回の統計教育の充実の背景には情報活用能力を統計の面で一層強化するねらいがあるとみてよい ([23])。上述のことを前提として、統計教育に期待することを課題として整理し、次の６項目にまとめる。ア｢人間ならではの強み｣を認識し、それに依拠した教育の文脈に明確に位置づけること。イ情報の賢い受信者と情報を創出する豊かな送信者の育成の両面を視野に入れること。ウ統計的な問題解決の過程｢問題－計画－データ－分析－結論」(PPDAC)の意味と必要性の理解及びその遂行に重点を置くこと。エ数学的活動を遂行できる資質･能力を育成する文脈で、数学的活動の過程や成果について多面的に考察したり、それらの妥当性について批判的に考察したりすることを重視している。これらが、③の統計的な問題解決の過程の文脈でも反映されること。オ統計に関する知識･技能は最小限にとどめ、習得した知識･技能を問題解決の過程で使いこなすことに重点を置くこと。カ統計的な問題解決の過程、とりわけ、｢問題｣及び｢結論｣の部分での問題設定や解釈では他教科や児童のかかわる合科的、教科横断的な諸活動との関連に配慮すること。３．プログラミング教育への対応｢世界に誇る日本の小学校教育の強みを生かしつつ、次世代に必要な資質･能力を、学校と地－18－
▲TOP

ページ： 22
域･社会の連携･協働の中で育むことができるよう、中央教育審議会における議論を踏まえつつ、小学校段階における資質･能力の育成とプログラミング教育の在り方について検討を行う｣ため ([24])、文部科学省は｢小学校段階における論理的思考力や創造性、問題解決能力等の育成とプログラミング教育に関する有識者会議｣を平成 28 年 4 月 19 日発足させ、今後のプログラミング教育の在り方について、小学校段階の教育に軸足をおいて検討を進め、｢議論の取りまとめ｣ ([25])を公表しているので、これに基づいて、プログラミング教育の方向性につて、プログラミング的思考と算数･数学科での対応について論点を整理することとする。 (1) プログラミング教育プログラミング教育は｢子供たちに、コンピュータに意図した処理を行うよう指示することができるということを体験させながら、発達の段階に即して、次のような資質・能力を育成するものである｣と規定され([25])、育成すべき資質・能力の三つの柱に対応させ、プログラミング教育をより具体的に次のように整理している。まず、「知識・技能」については学校種別に整理され、小学校では｢身近な生活でコンピュータが活用されていることや、問題の解決には必要な手順があることに気付くこと｣、中学校では｢社会におけるコンピュータの役割や影響を理解するとともに、簡単なプログラムを作成できるようにすること｣、高校では｢コンピュータの働きを科学的に理解するとともに、実際の問題解決にコンピュータを活用できるようにすること｣としている([26])。中高等学校では、特定の教科、技術･家庭科や情報科で教育内容として明示し、意図的、計画的に指導することになっている。次いで、｢思考力・判断力・表現力等｣については、｢発達の段階に即して、『プログラミング的思考』を育成する｣としている。最後に、｢学びに向かう力・人間性等｣については、｢発達の段階に即して、コンピュータの働きを、よりよい人生や社会づくりに生かそうとする態度を涵養すること｣としている。したがって、小学校段階におけるプログラミング教育は「身近な生活でコンピュータが活用されていることや問題の解決には必要な手順があることに気付き、プログラミング的思考を育成し、発達の段階に即して、コンピュータの働きをよりよい人生や社会づくりに生かそうとする態度を涵養すること」とまとめることができる。 (2) プログラミング的思考の育成｢プログラミング的思考｣は｢自分が意図する一連の活動を実現するために、どのような動きの組合せが必要であり、一つ一つの動きに対応した記号を、どのように組み合わせたらいいのか、記号の組合せをどのように改善していけば、より意図した活動に近づくのか、といったことを論理的に考えていく力｣と規定された([25])。この｢プログラミング的思考｣は新造語で、｢『コンピュテーショナル・シンキング』の考え方を踏まえつつ、プログラミングと論理的思考との関係を整理しながら定義され、｢プログラミングに携わる職業を目指す子供たちだけではなく、どのような進路を選択しどのような職業に就くとしても、これからの時代において共通に求められる力｣とされた。近年、学校内外での実施が進められているプログラミング教育では、｢論理的思考力や創造性、－19－
▲TOP

ページ： 23
問題解決能力といった資質･能力を育むという側面｣と｢コンピューターを動かすために必要なコーディング（プログラミング言語を用いた記述方法）を学ぶという側面｣があり、これら二つの側面の間の二項対立的な議論になりがちであったようである。こうした状況を打開し、両者に深く関わる概念として、上述のプログラミング的思考なる用語がつくられ、プログラミング教育の中核に位置付けられることとになったのである。 (3) 算数･数学科での対応当初、プログラミング教育と全ての教科・領域との関係を示すことも話題となったが、総合的な学習の時間、理科、音楽、図画工作、特別活動及び算数が取り上げられている。算数科では、｢計算することをプログラミングで教えること｣、｢文章題のストーリーをプログラミングによって単にアニメーション化すること｣を例示し、それらへの危惧を表明する分脈で整理されていた。 ① 計算の指導に関わって計算について、それは人間の文明が生み出した遺産である。例えば、｢筆算は数学の歴史の中で初期から存在したものではなく、長い年月をかけて人類が生み出したアルゴリズムであり、そうしたものを生み出す人間の数学的な思考が、人工知能の動きや働きなどを支えるおおもととなっているとみれば、これからの算数では、筆算が所与のものではなく、こうした意義を持つものであることなどを学ぶことが重要になる｣としている。すなわち、コンピュータ科学等でも用いられる「アルゴリズム」の典型として筆算を位置付け、｢問題を解決する手順を定式化して表したもの｣ととらえ、それを創り出す体験を筆算の学びを通して実現していくことが一層重要になろう。｢アルゴリズム｣を創る学びは、筆算など計算にかかわる内容にとどまらない、広く様々な内容と深くかかわっており上述の視点からの見直しと、それに基づく内容の取り扱いや授業の展開における革新が期待される。残念ながら、この部分は小学校学習指導要領解説算数編には引用されていない。 ② 文章題の指導にかかわって算数における文章題の解決は｢文章から数量の関係について情報を読み取り、それらの関係を明らかにし、解決の方法を立案して解決するという過程を体験する活動｣であり、数学的モデリングを実体験できる典型といえる。したがって、筆算や文章題は古くから算数の教材として位置付けられてきているが、時代の変化、その変化にともなう新たな要請に鑑み、それらを学ぶ意義を再点検し、それに相応しく授業を改善していくことが期待されていると言える。 ③ 算数･数学科での対応プログラミング教育の基本的な考え方は小学校段階に焦点を当てて整理されているが、数学科にも適用でることであり、上記ア、イにかかわることは数学科で取り上げる内容にも頻繁に登場するものであり、同様な対応が期待される。また、上述の数学的活動を充実させる文脈にのせて対応できれば、算数･数学科におけるプログラミング的思考の育成やプログラミング教育の実現がほぼできよう。流行におぼれることなく中長期的な展望のもとで冷静な対応が期待される。－20－
▲TOP

ページ： 24
おわりに今回の改訂は、戦後初めての出来事であるが、高大接続改革を動機として、従前の幼･小･中･高等学校へのボトム･アップでの改革ではなく、逆の方向、つまりトップ･ダウンでの改革が展開された。上述のように、算数的活動が数学的活動に統合されたり、算数科の内容領域の構成が数学科のそれに対応して再構成されたり、〔数学的活動〕のねじれが解消されたりしたのはその現れと言える。それほどに高等学校教育における授業改善が急務であることを物語っているところで、｢高等学校教育においては、スーパーサイエンスハイスクールにおける取組等を踏まえつつ、生徒の興味や進路に応じて、数学科の枠を越えた科学的なテーマに徹底的に向き合い考え抜く力を育成するため、大学入学者選抜の改革や｢大学入学希望者学力評価テスト(仮称)｣に向けた動きも踏まえつつ、数学と理科の知識や技能を総合的に活用して主体的な探究活動を行う新たな選択科目｢数理探究(仮称)｣の設置を検討することが求められる。｣([2])として、高等学校数学科での新科目｢数理探究(仮称)｣の設定が提案されていた。ここで、｢大学入学希望者学力評価テスト(仮称） )は、現行の｢大学入試センター試験に代わるテスト｣の当時の名称(案) であったが、現時点では｢大学入学共通テスト(仮称)｣(以下、共通テストとする)とされている。このテストは｢現行｣のもとでは平成 32 年度(平成 33 年度入学者選抜)から、｢次期｣のもとでは平成 36 年度(平成 37 年度入学者選抜)から実施される予定になっている。大学入試センターからは先日問題案が公表されている([24])が、一部問題で記述式が採用され、記述式問題は、出題科目｢数学Ⅰ｣と｢数学Ⅰ・数学Ａ｣で、出題範囲は｢数学Ⅰ｣の内容とするとしている。したがって、高等学校数学科での新科目｢数理探究(仮称)｣の設定の提案([2])を受けての新科目｢理数探究｣及び｢理数探究基礎｣(高等学校理数科として位置づけられる)を設定することとなっている。しかし、それらが共通テストに直接かかわることは、当面ない状況である。 (*)本稿は、清水静海｢最新教育情報：算数科が育成を目指す資質・能力の構成と教育内容への反映 ― 新学習指導要領の特色と課題（その１） ―」、新算数教育研究会編集『新しい算数研究』、 4 月号、 no.555、H29.4.1、pp4-5.)及び清水静海｢最新教育情報：数学的活動の充実 ― 新学習指導要領の特色と課題（その２）―｣、新算数教育研究会編集『新しい算数研究』、5 月号、no.556、H29.5.1、pp45.)、及び清水静海｢育成を目指す資質・能力と授業改善 ― 算数・数学 ―｣(広報誌『Rimse』、 No.19(2017.6.20 発行)｢特集：新学習指導要領が目指すこれからの理数科教育Ⅰ｣)をもとに、加除、再構成したものである。引用・参考文献等 [1]文部科学省｢小中学校学習指導要領｣(H29.3.31)。 [2]教育課程企画特別部会｢論点整理｣(H27.8.21)。 [3]中央教育審議会｢幼稚園、小学校、中学校、高等学校及び特別支援学校の学習指導要領等の改善及び必要な方策等について｣(答申、H28.12.21)。 [4]指導事項は各領域の(1)、(2)、(3)、・・・の項目を指す。－21－
▲TOP

ページ： 25
[5] ｢クリエイティブな素養を育むプログラミング教育の可能性｣(新春座談会)、『日本情報産業新聞』、2375 号、6～8 面(H29.1)。 [6]G.Polya,“Induction and plausible reasoning” 、1954. [7]H1 改訂小学校学習指導要領。 [8]文部科学大臣｢諮問理由の説明｣(H26.11.20)。 [9]産経新聞朝刊正論｢若い世代に求めたい新しい知性｣(H29.1.3)。 [10]Ｇ７倉敷宣言(教育大臣会合：H28.5.15) [11][2]と[3]の【概要】。 [12]H10.12.公示。 [13]英訳(仮訳)は文科省ホームページで公開されている。 [14]関係者の後日談によると、審議の過程で｢生きる力｣とするか｢生き抜く力｣とするかで活発な議論があったようである。 [15]｢現行｣の英訳(仮訳)版では’zest for life’とされている。 [16]｢現行｣の解説では、算数科では算数的活動の定義の末尾を｢活動｣としているが、数学科のように｢営み｣とした方がよい。 [17]中学校学習指導要領解説数学編。 [18]高校の｢数学Ⅰ｣(必履修科目)につなげ、10 カ年間で対応の予定。 [19]中教審教育課程部会｢算数・数学ワーキンググループにおける審議の取りまとめ｣(H28.8.26)。 [20]これと同趣旨で、小学校算数及び高等学校数学についての例示がなされている。 [21]資料６｢小・中・高等学校を通じた統計教育のイメージ、内容等の整理(案)｣(H28.5.13.第七回 WG)。 [22]これは、英国連邦圏を中心として初等中等教育の数学教育に導入されている課題解決の手順で、総務省ホームページで｢統計を使った問題の発見から解決まで｣として公開されているものに基づいている。 [23]清水静海｢統計教育への６つの期待｣、『算数授業論究』、vol.112、pp2-3。 [24]｢小学校段階における論理的思考力や創造性、問題解決能力等の育成とプログラミング教育に関する有識者会議(平成 28 年 4 月 19 日初等中等教育局長決定)。 [25]「小学校段階における論理的思考力や創造性、問題解決能力等の育成とプログラミング教育に関する有識者会議」(H28.4.19.設置)が｢小学校段階におけるプログラミング教育の在り方について (議論の取りまとめ)｣(H28.6.16、以下、｢とりまとめ｣とする。)を公表した。 [26]中高等学校では、特定の教科、技術･家庭科や情報科で教育内容として明示し、意図的、計画的に指導することになっている。 [27]大学入試センター「大学入学共通テスト(仮称)」記述式問題のモデル問題例。－22－
▲TOP

ページ： 26
数学の科学・工学分野への適用調査学習数学研究所中村要約科学や工学の各分野でどのような数学の内容・手法が適用されているかという一連の調査を実施し、俯瞰チャート（関連マトリックス）が作成でき一定の成果が得られたので報告する。キーワード:数学、俯瞰チャート、STEM 教育１．はじめに数学が、科学や工学の分野で広く活用されていることはいう疑う余地はないが、具体的に物理学などの科学や、機械工学、電気工学、建築・土木工学といった各種工学の分野で、数学のどのような内容・手法が適用されているかという調査を実施し、ある程度まとまったので報告する。２．調査方法数学 ⇔ 科学 ⇔ 工学の３つの領域においてそのような関連があるかを、各種文献やネット情報からの検索などでまとめた図が、全体俯瞰マップである。数学の様々な分野・手法が、物理学などの科学の分野や各種工学の分野と複雑に絡みあいながらも、非常に密接な関係があることがわかる。一見、秩序立っていない混とんとした図と思われるが、適用分野に応じて数学が電気系、力学系、情報系、金融系の大きく４つの分野に関連づけられるように考えられる。特に、電気系、力学系は物理学をインタフェースとして経由しながら、建築・土木・機械工学、電気工学などの工学へ関連しており、情報系に関しては、科学系のフィールドとして情報科学を経由して、情報・通信工学と結びついている。また制御理論も制御工学に関連するとして、力学系へ組み入れたが、情報系へ組み込んだ方がベターかもしれない。また、金融系も数理ファイナンスを経て、金融工学へ関連していると思われる。３．調査結果次に４分野、すなわち、力学系、電気系、情報系、金融系における数学とは具体的に何か、各分野を構成するそれぞれの要素が中学、高校、大学で学ぶ数学のどの内容（単元）と関係づけられるか、すなわちどのようにマッピングされているかを詳細に調べて、４個の関連マトリックスを作成した。力－23－
▲TOP

ページ： 27
（１）力学系数学古典力学（ニュートン力学）、解析力学、熱力学、制御理論の４分野と数学の関係をマトリックスにした（図表１：力学系数学俯瞰チャート）。 ①古典力学（ニュートン力学）質点の力学では、微分・積分、ベクトル（解析）、微分方程式が主であり、時間ｔを１変数とする位置座標に関する微積分や常微分方程式が主である。質点から剛体、弾性体・流体といった連続体を扱う力学になると、点としていた物体から大きさのある物体として扱うようになるので、単なる質量が重積分で求められる慣性モーメントにシフトする。また、３次元のベクトルで表わせた力は連続体ではテンソルに、連続体の場を支配する方程式は偏微分方程式のナビエ・ストークスの方程式が用いられるようになる。 ②解析力学解析力学では変分の考えが支配的で、ハミルトン力学、ラグランジュ力学といった、偏微分（方程式）が主に使われ、正準変換、ルジャンドル変換も出てくる。 ③熱力学熱力学では、熱的なマクロな現象をマクロ的手法で解明するため、それほど高度な数学は出てこない。ただ、エントロピーなどやや（抽象的かつ哲学的）概念ともいえる状態変数と熱力学的変数において、ルジャンドル変換や偏微分、全微分、完全微分と関連してくる。熱力学と異なり、熱的なマクロな現象をミクロな視点（統計的）手法で探るのが統計力学であり、この分野の調査を継続させたい。 ④制御理論制御理論に関しては、古典制御と現代制御に大きく二分され、古典制御理論ではシステムの入力と出力だけに注目したラプラス変換よる機械的な計算が主であるが、現代制御理論では、システムの入力と出力だけでなく、システムの内部状態も変数にした行列（線形代数）を含んだ状態方程式を扱い、数学的にも高度かつ複雑になる。さらにシステムの安定性基準に関して行列演算や最適理論など高度な数学的理論が出てくる。（２）電気系数学直流（定常電流）、交流と交流理論、電気と磁気（電磁気学）の３分野と数学の関係を調査し、マトリックスにした（図表２：電気系数学俯瞰チャート）。 ①直流（定常電流）直流（定常電流）はオームの法則、その拡張版であるキルヒホッフの法則が主で、大方中学数学で理解できる内容であるが、連立方程式で解く計算では線形代数を知っていた方がベターな場合もある。 ②交流と交流理論交流と交流理論では、三角関数、ベクトル、複素数といった高校数学が必要になってくる。－24－
▲TOP

ページ： 28
交流理論では常微分方程式やその解法であるラプラス変換に一部関連してくる。 ③電気と磁気（電磁気学）電気と磁気（電磁気学）では高度な大学数学が必要になってくる。微積分（偏微分、重積分も含めて）は勿論、ベクトル解析そして電磁気学の集大成であるマクスウエル方程式では偏微分方程式が関連してくる。（３）情報系数学情報通信理論、情報数学・離散数学、多変量統計解析と数学との関連も調査した（図表３：情報系数学俯瞰チャート）。 ①情報通信理論情報通信理論は、熱力学で出てきたエントロピーと関連し、力学系高校レベルの数学では、特に情報エントロピーを表す対数が主に使われる。通信路符号化では確率や線形代数にも関連してくる。ただ、符号化理論では、ガロア拡大体といった代数学の知識が必要になってくる。 ②情報数学・離散数学おもに集合と論理、グラフ理論などの離散数学自体に関連する。 ③多変量統計解析多変量統計解析は、従来からの古典的手法で、統計学や線形代数が主である。この領域はダイナミックに変動している。今後、現代流行のデータサイエンスや人工知能と関連し、非常に活性化する領域でもあり、調査を継続したいと考えている。（４）金融系数学証券投資理論、財務分析（コーポレートファイナンス）、経済理論と数学の関連も調査した（図表４：金融工学／経済学俯瞰チャート）。証券投資理論では、中学数学の内容はいうまでもなく統計学を含んだ高校レベルの非常に広範な数学に関連してくる。さらに金融派生商品の投資になると、デリバティブ価格をブラックショールズ式では、確率過程を含んだ非常に高度な確率微分方程式（非線形偏微分方程式）が登場してくる。また、財務分析（コーポレートファイナンス）、経済理論にも数学が使われ、特に後者では経済学という文系の領域でありながら数学が大いに関連している。４．結語今回の調査において４つの数学系にまとめたが、考え方次第では、電気系、力学系をひとつにすべきなど他に様々な分類の仕方があるかもしれない。ただ分類の方法でいろいろ考えても次のステップに進めないので、今回は便宜上４つに分類し、それぞれの単元・内容がどの数学要素にマッピングされているかを調査した。－25－
▲TOP

ページ： 29
４分野のどの分野をとってもそれぞれ特徴や個性はありながらも、数学と密接な関係にあり、全分野とも数学抜きでは学問体系は成り立たないといっても過言でない。また、この４分野はそれぞれ独立しているわけではなく、例えば、力学と電気系（電磁気学）とは今回の調査では便宜上分けたが、 F  qE （ F ：力, ） q ：電荷， E ：電場（電界）という関係式で互いに関連付けられる。このように底流となっている数学を通じて４つの調査分野はお互い関連し合っている事実も興味深いと思われる。５．今後の予定今後は力学系や電気系で今回は含まれていない、高度な物理学の内容である量子力学、統計力学、相対性理論予定である。量子力学、統計力学は半導体など物性（マテリアル）に関連し、さらに量子力学は未来の量子計算機ともいわれる量子コンピュータなど情報理論とも関連してくる。相対性理論は実用的には GPS や衛星での計測に関連してくるが、宇宙・天体の起源、重力波、素粒子の起源など夢とロマンにあふれた分野でもあるので、その領域を記述する数学は一体何か、おおいなるモチベーションを保ちつつ調査・研究してみたいと思う。さらに、情報系において現在流行のデータサイエンス、人工知能（機械学習、深層学習 etc）がどのような数学と関連しているのかも調査を進める予定である。これらの調査作業を通じて、数学が数理科学や情報科学など、また工学の分野とどう関連し合っているか見極め、さらに STEM 教育の観点から提言できることはないかを考察していきたい。引用・参考文献 ⑴「力学系数学」関連 [1]小出昭一郎 [2]砂川重信 [3]原康夫 [4]山内恭彦 [5]伊藤克司 [6]砂川重信 [7]戸田盛和物理学裳華房 1997 年（※）（※）（※）に対しても調査を行って、俯瞰チャート（マトリックス）にまとめ上げる力学の考え方物理学基礎一般力学解析力学岩波書店 1993 年 2016 年 2002 年学術図書出版岩波書店講談社 2009 年 1993 年 1983 年講談社 2010 年講談社 2012 年熱・統計力学の考え方熱・統計力学岩波書店 [8]佐藤和也、平元和彦、平田研二 [9]佐藤和也、下本陽一、熊澤典良はじめての制御工学はじめての現代制御理論－26－
▲TOP

ページ： 30
[10]橋技術科学大学高等専門学校制御工学教育連携プロジェクト [11]藤川英司 [12]川崎晴久鈴木勝正他制御理論の基礎と応用森北出版制御工学 1995 年実教出版 2017 年産業図書 1991 年ロボット工学の基礎 ⑵「電気系数学」関連 [13]砂川重信 [14]高橋秀俊電磁気学の考え方電磁気学裳華房電気磁気学岩波書店 1959 年電気学会 2002 年 1993 年 [15]山田直平・桂井誠 [16]砂川重信理論電磁気学紀伊国屋書店 1999 年（１）における（※）の書籍も参考にした ⑶「情報系数学」関連 [17]先名健一例題で学ぶ符号理論入門森北出版 2011 年 2011 年 [18] 稲井寛はじめての情報理論森北出版 [19]佐藤洋 [20]宮川洋情報理論情報理論裳華房コロナ社 1983 年 1979 年 [21]寺田文行他 [22]河口至商情報数学の基礎多変量解析入門サイエンス社 1973 年 1999 年 ⑷「金融系数学」関連 [23]石野雄一道具としてのファイナンス日本実業出版社 2005 年日本経済新聞出版社 2015 年 [24]デービッド・ G.ルーエンバーガー , 今野浩他 [25]木島正明 [26]木島正明他金融工学日本経済新聞出版社金融工学入門 2002 年 2012 年朝倉書店 2011 年 2009 年 2009 年 1999 年ファイナンス理論入門朝倉書店 [27]木島正明、岩城秀樹 [28]手嶋宣之 [29]滝川好夫 [30]滝川好夫経済と金融工学の基礎数学ダイヤモンド社ファイナンス入門たのしく学ぶミクロ経済学たのしく学ぶマクロ経済学ミネルヴァ書房ミネルヴァ書房－27－
▲TOP

ページ： 31
「縮図や拡大図」地図上の実際の長さを求めるときに見られる誤答－算数検定６級の答案の分析を通して－学習数学研究所松本精一要約 2017年8月8日第99回全国算数・数学教育研究（和歌山）大会幼稚園・小学校部会において、「実用数学技能検定（算数検定）の答案の考察５」と題した研究発表を行った。本稿は、このときの研究をもとに答案の調査分析を進めて再構成したものである。実用数学技能検定（算数検定）の６級に出題した「縮図」の問題について、採点システムの誤答分析機能を用いて、解答類型別に反応率を調査集計した。調査の結果、縮図上での長さから実際の長さを求めるときにもっとも多い誤りは、単位を変換するときに生じることが分かった。日常生活において単位は非常に重要であるので、常に単位を意識して生活する習慣を身につけることが大切であると考えられる。キーワード：縮図、縮尺、単位変換１研究のねらい（はじめに）小学校算数科第６学年の目標に「(3)縮図や拡大図、対称な図形について理解し、図形についての理解を深める。」（文部科学省「小学校学習指導要領解説算数編」2008 年）とある。縮図や拡大図については、まず図形の合同との関連で、中学校第３学年で学習する相似の理解の基礎として、図形を考察し理解を深め、図形に対する感性を豊かにすることをねらいとしいている。さらに、身の回りから縮図や拡大図を見付ける活動をとおして、日常生活の中で縮図や拡大図を進んで活用しようとする態度を育てることをねらいとしている。実用数学技能検定（算数検定）（以下「算数検定」という。）の６級の出題範囲は小学校第６学年及び第５学年程度であり、受検者の多くは小学校６年生である。したがって、６級の答案を分析することによって、小学校第６学年の児童のおおよその理解度がわかる。６級で出題した縮図や拡大図に関する問題を見ると、三角形、四角形の縮小拡大の問題についてはほとんどの問題が正答率 90％以上であり、縮小拡大の倍率や対応する辺の長さを求める基本的な内容については理解していることがわかる。一方、日常の生活と関連した地図の縮尺を扱った問題では正答率が低くなる。この傾向から、縮尺を用いて実際の長さを求める問題に焦点をあて、受検者の答案から、つまずきがどこで起こるかを分析しようと考えた。－28－
▲TOP

ページ： 32
２研究の内容地図はもっとも身近にあり有益な縮図である。地図を活用することによって、２地点間の距離、道のりや道順、ある区域の広さ等を知ることができる。地図を正しく理解して活用するために、縮図について学習することは非常に重要である。次の縮図に関する問題は、算数検定６級に出題した問題である。・第 299 回（平成 29 年 2 月 17 日実施）１２５００しゅくず右の図は、の縮図です。広場は長方形たての形をしていて、地図上では、縦２cm、横３.５cm になっています。これについて、次の問題に答えましょう。じっさい（測定技能）（26）（27）（28）広場の実際の縦の長さは何 m ですか。広場の実際の横の長さは何 m ですか。めんせきたんい広場の実際の面積は何 m2 ですか。単位をつけて答えましょう。・第 283 回（平成 28 年 2 月 13 日実施）１２０００しゅくあやこさんは学校のしき地を、右の図のようなずたての縮図でかきました。この縮図で、体育館は縦１.５cm、横２cm の長方形で表されています。次の問題に答えましょう。（測定技能）じっさい（27）（28）体育館の縦の実際の長さは何 m ですか。めんせき体育館の実際の面積は何 m2 ですか。この問題は、計算の途中の式と答えを書きましょう。第 299 回の（26）、（27）及び第 283 回の（27）の問題の主旨は、地図上の長さと縮尺を用いて実際の長さを計算で求めることができるかを観ることにある。算数検定の問題の正答率は 70％以上のものが多く、正答率 60％以上にまで範囲を広げるとほとんどの問題がこれに含まれる。このことを考えると、第 299 回（26）58.2％、（27） 53.2％、第 283 回（27）63.3％という正答率から、これらの問題は標準よりやや難しい問題に位置するといえる。－29－
▲TOP

ページ： 33
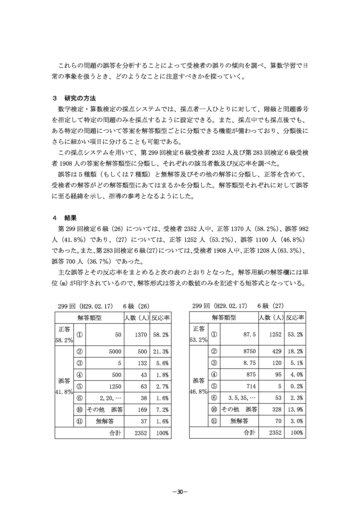
これらの問題の誤答を分析することによって受検者の誤りの傾向を調べ、算数学習で日常の事象を扱うとき、どのようなことに注意すべきかを探っていく。３研究の方法数学検定・算数検定の採点システムでは、採点者一人ひとりに対して、階級と問題番号を指定して特定の問題のみを採点するように設定できる。また、採点中でも採点後でも、ある特定の問題について答案を解答類型ごとに分類できる機能が備わっており、分類後にさらに細かい項目に分けることも可能である。この採点システムを用いて、第 299 回検定６級受検者 2352 人及び第 283 回検定６級受検者 1908 人の答案を解答類型に分類し、それぞれの該当者数及び反応率を調べた。誤答は５種類（もしくは７種類）と無解答及びその他の解答に分類し、正答を含めて、受検者の解答がどの解答類型にあてはまるかを分類した。解答類型それぞれに対して誤答に至る経緯を示し、指導の参考となるようにした。４結果第 299 回検定６級（26）については、受検者 2352 人中、正答 1370 人（58.2％）、誤答 982 人（41.8％）であり、（27）については、正答 1252 人（53.2％）、誤答 1100 人（46.8％）であった。また、第 283 回検定６級（27）については、受検者 1908 人中、正答 1208 人（63.3％）、誤答 700 人（36.7％）であった。主な誤答とその反応率をまとめると次の表のとおりとなった。解答用紙の解答欄には単位（m）が印字されているので、解答形式は答えの数値のみを記述する短答式となっている。 299 回（H29.02.17）解答類型正答 58.2％ ① ② ③ ④ 誤答 41.8％ ⑤ ⑥ 50 5000 5 500 1250 2,20,… 誤答 6 級（26）人数（人）反応率 1370 500 132 43 63 38 169 37 2352 58.2% 21.3% 5.6% 1.8% 2.7% 1.6% 7.2% 1.6% 100% 299 回（H29.02.17）解答類型正答 53.2％ ① ② ③ ④ 誤答 46.8％ ⑤ ⑥ 87.5 8750 8.75 875 714 3.5,35,… 誤答 6 級（27）人数（人）反応率 1252 429 120 95 5 53 328 70 2352 53.2% 18.2% 5.1% 4.0% 0.2% 2.3% 13.9% 3.0% 100% ⑩ その他 ⑪ ⑩ その他 ⑪ 無解答合計無解答合計－30－
▲TOP

ページ： 34
それぞれの解答類型について、正答についてはその求め方、誤答については誤答にいたる経緯を考えると、次のようになる。解答にいたる経緯については、解答類型① から⑥までは第 299 回の（26）で例示した。また、解答類型⑦及び⑧は第 283 回（27）のみで調査したためこの問題で考えた。解答類型①は正答である。正答にいたる過程は、次の㋐、㋑の２つの段階が考えられる。㋐「地図上の長さ（ cm）と縮尺を用いて cm の単位で実際の長さを求める」㋑「㋐の値をｍに変換する」第 299 回（26）では ①２×2500＝5000、5000cm＝50ｍ解答類型②は、㋐までは求められたが、㋑を考慮しないで答えとしたものと考えられる。 ②5000cm→5000ｍ 283 回（H28.02.13）解答類型正答 63.3％ ① ② ③ ④ ⑤ 誤答 36.7％ ⑥ ⑦ 30 3000 3 300 1333 1.5,15,… 40 6 級（27）人数（人）反応率 1208 304 83 85 1 49 12 14 117 35 1908 63.3% 15.9% 4.4% 4.5% 0.1% 2.6% 0.6% 0.7% 6.1% 1.8% 100% ⑧ 400,4000,… ⑩ その他 ⑪ 誤答無解答合計解答類型③及び④は、おそらく㋐までは求められたが、㋑で誤ったと考えられる。③は 1000cm→1ｍとしたもの、④は 10cm→1ｍとしたものと思われる。 ③5000cm→5ｍ、④5000cm→500ｍ解答類型⑤は、縮尺の分母の数値を地図上の長さで割ったと考えられる。これは㋐の段階での誤りである。 ⑤2500÷２＝1250 解答類型⑥は、地図上の長さの数値をそのまま答えとした、あるいはそれを単位換算したと考えられる。これらは㋐の段階より前の段階での誤りである。 ⑥２ｍ、20ｍ、200ｍ、… 283 回（27）の解答類型⑦は、縦の長さを求めるところを、横の長さを求めてしまったと考えられる。実際の長さを求める方法は理解しているが、問題を読み間違えている。 ⑦２×2000＝4000、4000cｍ＝40ｍ解答類型⑧は、横の長さを求め、単位換算を誤ったものと考えられる。これは㋐の段階までは理解しているが、問題の読み間違いと㋑ができていない。 ⑧4000cm→400ｍ、 4000cm→4000ｍ、･･･－31－
▲TOP

ページ： 35
５考察解答類型②の反応率はおよそ 15％～20％であり、誤答でもっとも多かった。これらの受検者は単位の変換を忘れたかあるいは、もともと単位を変換することを意識しなかったと考えられる。解答類型③、④の反応率を合わせると、およそ７～9％であり、これらの受検者は単位変換をしようとしたが誤ったと考えられる。解答類型③は１km＝1000ｍと混同し、解答類型 ④は 1cm＝10mm などと混同したものと考えられる。解答類型②～④は地図上の長さと縮尺の関係については理解していると考えられる。解答類型⑤は第 299 回（26）のように、商が整数で表されるもので反応率が高く、第 299 回（27）、第 283 回（27）のように割り切れない場合、反応率は非常に低い。解答類型⑥は縮尺を用いないで、実際の長さを求めようとする誤答である。また、解答類型⑤、⑥は、地図上の長さと縮尺の関係を理解していない誤答である。解答類型⑦、⑧は求める箇所を誤ったものである。地図上の長さと縮尺の関係は理解していると考えられる。第 299 回では、（26）で縦の長さ、（27）で横の長さと別々の小問で問われているので、この類型の誤りは発生していない。６まとめ解答類型①（正答）及び解答類型②③④（誤答）を見ると、実際の長さを求めるためには、縮図上の長さに縮尺の逆数をかければよい（もしくは縮図上の長さを縮尺で割ればよい）ことを、80％以上の受検者が理解していることがわかる。しかし、25％～30％の受検者は単位換算をしなかったり、誤ったりしている。身の回りには様々な量を表す単位が用いられている。メートル法における単位の相互関係を理解し正しく換算することは、日常生活や社会生活を送るうえで非常に重要であるので、日頃から意識して学習することが求められる。解答類型⑤⑥にあてはまる受検者は、地図上の長さと縮尺、実際の長さの関係がわかっていないので、地図が生活の中で重要であることを認識し、地図に関心を持ち正しく読めるようにすることが必要である。解答類型⑦⑧にあてはまる受検者は、問題文を注意深く読み取り、求められている解答がどのような意味をもつかを理解することが必要である。引用・参考文献 [1]文部科学省「小学校学習指導要領解説算数編」2008 年 [2]松本精一「実用数学技能検定（算数検定）の答案の考察５」，公益社団法人日本数学教育学会日本数学教育学会誌，第 99 回大会特集号 2017 年（和歌山大会），pp229，2017 年 [3]公益財団法人日本数学検定協会「第 299 回実用数学技能検定（算数検定）６級」 [4]公益財団法人日本数学検定協会「第 283 回実用数学技能検定（算数検定）６級」 2017 年 2016 年－32－
▲TOP

ページ： 36
「3.1＋5.9」についての扱い学習数学研究所渡辺信要約社会が算数・数学に興味関心を示すことは少ない。しかし、多くの人々が 3.1＋5.9 の計算結果に関心を示した。小学校の算数では９という答えを正しいとしてきたにもかかわらず、その後の人生経験から 9.0 が正しいと思うようになっている。今回の算数に対する話題は、子供の算数のテスト結果・成績にしか関心がないことの表れでもあるが、算数の中に含まれる曖昧さについて考えさせられた。数学検定の結果の調査を踏まえ、この 3.1＋5.9 に対する関心調査を報告する。キーワード：算数教育有効数字算数の中に潜むあいまいさ１．問題の所在「3.1+5.9」の答えは９か 9,0 かで社会問題になり、ネット上を騒がせた。この答えとして正しいのは９か 9.0 かが、多くの意見をつけてメール上で飛び交っていた。関心があるのは 40 歳代の小学生の保護者ではなかったかと思われる。問題の出発点は、小学校のある先生が、生徒の答案 9.0 に対して、丸を付けなかったことに、その答案を見た保護者からの問題指摘から始まった。この計算問題の正解は何かについて、テレビで取り上げたところ、正解は何かの判定が出来ず、｢日本数学検定協会｣なら、どのように扱うかの問い合わせがこの論文の問題の発端である。この問い合わせについて、｢日本数学検定協会｣では、どちらも正解とコメントを出した。このコメントに対して、一般社会人の数学感覚では、「算数・数学の問題の答えは唯一決まる」と考えているので、一般社会人に対する答えには遠い感じがした。小学校の算数授業では、多くの人々は答えは９と教えられてきていても、その後の数字の扱いにおいて、答えは 9.0 にしたいのではなかろうか。算数・数学教育の変化の中で理解している人々にとって、答えがどちらも正解ということに対して納得性に乏しかった感じがした。現在の学校教育では、先生方はこの答えとして、9 と教えているので、教室での指導では９が正解になる。小学校の教科書では 9 が正解と教科書に書いてあるので、9.0 とは教えていないという小学校の先生からも、9.0 として方が良いのではないかという声も聞こえてきた。また、有効数字を考えることが重要で 9 では教育が間違っているのではないかという工学系の方からの指摘もあった。｢日本数学検定協会｣の扱いについてのコメントは、小学生は 9 として学び、その後測定値として扱う場合には 9.0 としなくては誤りとする立場など、いろいろな考え方があるので、一概に 9 とも 9.0 とも決められないことを前提にして、どちらの答えも正解として扱っていることをコメントした。しかし、社会では 9 か 9.0 かは、算数・数学教育にも大きな問題として解決できないままに、いろいろな考え方があるようであった。この問題に対して、いろいろな意見を聞くために、いくつかの学会で研究発表として取り上げてもらい、この問題についての意見を聞くことが出来た。数学検定協会として次の学会等でこの問題について触れ、意見を求めた。－33－
▲TOP

ページ： 37
Nｏ．１２３４５６７８９ 10 11 12 13 14 日付 11/27 12/25 1/3 1/28 1/19 1/20 3/12 3/18 3/13 4/1 4/9 4/13 8/8 8/8 コメント内容(第) テレビ朝日取材 3.1＋5.9 の答えはいくつ？ご質問の解答 3.1＋5.9 の答えはいくつ？ 3.1＋5.9=？談話会での投稿(テレビ番組) 検定問題調査数学教育におけるあいまいな用語とその対処数学教育の目標 Number sense を調べることの指摘 3.1＋5.9 再考 3.1＋5.9 の指導について有効数字をいかに扱うか(高専) 3.1＋5.9 の指導についてー正解は 9.0 か 9 かー表取り扱い場所日本数学検定協会数学教育談話会一松先生談話全国数学教育学会水戸数学の会数学教育談話会調査日本科学教育学会日本科学教育学会講義談話備考 4/15 調査活用数学教育談話会日本数学教育学会日本数学教育学会日本数学教育学会調査活用 8/7 3.1＋5.9 についての話題提供２．この問題に対してのアンケート結果要約テレビ放送においてもアンケートは多くの人に聞いてみたようだった。そしてテレビが行った回答でのアンケートでも９と 9.0 の二つに意見が割れた結果を示していた。そこで、いくつかの視点からこの問題に関するアンケートを行い、正解は何かについての意見を求めた結果を示す。（１）年齢からみた答えの違い 70 歳以上の人は 9.0 と答えた 30 歳以下の人は９であった年齢の違いがこの答えに対してはっきりと分かれたのは興味深い結果となった。中間層では答えに対してあいまいであったのは、算数・数学教育の影響と社会での利用についての判断不可能が影響しているかもしれない。これから先生になろうとしている小学校教員養成の課程にいる学生はほとんど 9 で出会ったことは、教科書に従って学んでいることをも示していた。（２）職業からみた答えの違い理系（技術職）の職業の人は 9.0 で有効数字が理由と答えた。文系（経理職・経済分野）の人は９が好ましいという。理系の若い人も 9.0 であったことは職業柄数字をいかに見ているかという違いがある。経済・経営関係の仕事についている人々の答えが９であることには興味がありました。（３）海外ではどのようになっているか ATCM(アジアにおける数学とテクノロジーの国際会議)で、この問題にどのような反応を示すかを聞いてみた。約 20 カ国の数学者・教師は 9.0 が圧倒的に多かったのは集まっている先生方が理系の Technology を積極的に用いる方面の人であったので、日本と同じであっても不思議ではな－34－
▲TOP

ページ： 38
い。そこで、この数値に単位を付けて、｢3.1 ドルと 5.9 ドルの和は 9 ﾄﾞﾙか、9.0 ドルか｣の問題に変えたところ、今度の答えは 9 ドルと答えがかわった。9.0 ドルとは言わないと、9.0 には否定的であった今までの自分の立場に対して、異なった考え方をしていることに気が付いて興味を持ちちながら、どちらが正回科の判定は出来なかった。各自の学校教育の答えはどちらが正しいかについては明確な答えはえられなかったので、教育の問題ではあいまいさがどこ国ででも残っているようでした。この問題に対して個人として問題には非常に興味を持ったという反応が日本の国内だけではなく、多くの国できちんとは決めていないこととして扱っていると考えられる。（４）その他の興味あること・電卓ではどのような結果が出てくるかという問題に対して、この問いかけに即答した人はほとんどいなかった。そして自分の持っている電卓で確かめてみたいとは言ってはいても実行した人は少ない。スマホにある電卓ですぐに確認しようとした人はいなかった。スマホにある電卓には関心を示さなかった。また数値にたいする関心も低いことが分かった。・テレビ番組で見る数字としてスポーツの記録を問題にした人がいた。駅伝で使われている数値を考え、0 の扱いに興味を持った人、スキージャンプではと考えたときに０の必要性を重視していたが、実際に 0 が付いているかは確認している人はほとんどいなかった。テレビで見る数字に関心を示しているとは考えられず、ただ聞き流してしまうのではないかと思われた。・日経平均、トピックスなどの数値を想った人もいたが、この数値が何を意味するのか答えられた人はいなかった。何となく眺めている数値では何も解決できないことを知らされました。・天気予防の温度数値について、今日の測定値では最高気温は小数点以下一桁をしましますが、明日の朝の最低気温については小数点以下の発表がないことにも気が付いていない。このことは測定値では 15.0 もあるのですが、予想地では 15 になっていることを聞いて不思議がっていた。測定値はどこまで正しいか、予想が出来る範囲はどこまでかをも数値は語っていることにもっと注目してもよいと思われた。３．この問題に対する意見の集約（１）日本数学検定協会の見解・・・結論は９も 9.0 も正解にする検定ではテストの結果しか見ることができず、どのような条件のもとで答えを出したかわからない。小学生ならば教室で教えられていることとして答えるであろう。また技術者ならば単位も考えて有効数字で答える可能性がある。回答した人の立場がわからないので、採点においては両方ともに正解とみなす。（２）ある有名な数学者の見解・・・結論は９も 9.0 も正解にするどちらが正解かは答えを求めている人がどのような条件で答えを要求しているかによって違う。最も簡単な数値で答える場合は 9 が正解。有効数値ならば 9.0 が正解であるが、今回の場合はなにも条件が示されていない。ある意味では答えられないとしているのではないかとも思えた。（３）小学校の先生の見解・・・当然 9 が正解現在の学校教育ではこの問題は小学校 3 年でいの学習内容で、教科書には次のように書かれている。教室では９と教えているので、この問題に対しては 9 と答えて欲しい。－35－
▲TOP

ページ： 39
しかし、学年が進むと数値の考え方が変わる可能性があり、その時々の授業によって正解が変わる。問題になったテストでの原点をした先生は授業ではいかに教えたかを重視したのであろう。子供たちにとって 9 が正解ということは学校教育によりどころを求めている。（４）技術者の見解・・・9.0 が正解有効数字の重要性を強調した。ものを測るときに、3.1cm としたときにその物は 3.04≦もの＜3.05 という範囲にある。これが 9 になった場合は 9.4 数学者＜9.5 と解釈され、9.0 の場合は 9.04≦もの＜9.05 となる。いかに正確に計っているかが問題であり、おの重要性を強調すべきである。しかしただの計算ではどうなるかについてはわからなかった。（５）ある数学者の見解・・・９が正解 3.1+5.9 の問題を分数表示した場合を考えた。 3.1＋5.9＝31/10＋59/10＝90/10＝９（６）ある数学者の見解・・・９.0 か９．でもよい（７）経済人が上げた例からの見解・・・９が正解日本のお金は日常「円」しか使わないのでドルで説明したいと前置きして、3.1 ドルとは 3 ドル 10 セントのことである。よって、3．1 ドル＋5.9 ドルの答えは 9.0 ドルとは言わない。9 ドルが正解とした。４．数学検定での調査この問題に対して、検定問題ではどのような答えを提示するかを調べた結果がある。しかし、この問題では数値に単位が付いているので、計算問題だけの結果とは異なる可能性があることも今日慮しなくてはいけない。この問題はテレビで取り上げた後に実施された。社会的に問題になっていたことに対して、検定受検者は小学生が大半であまり関心を示さなかった。「3.1＋5.9 問題」は大人の間での興味関心が高かったといえる。問題(検定299回９級(15)) たくやさんのクラスでは，６月と７月に空きかん拾いをしました。全員で拾った空きかんの重さは，６月は３.７kg，７月は５.３kg でした。６月と７月に拾った空きかんの重さは，合わせて何kg ですか。たんいをつけて答えましょう。問題の正答９Kg 9.0Kg (どちらも正解とする) －36－
▲TOP

ページ： 40
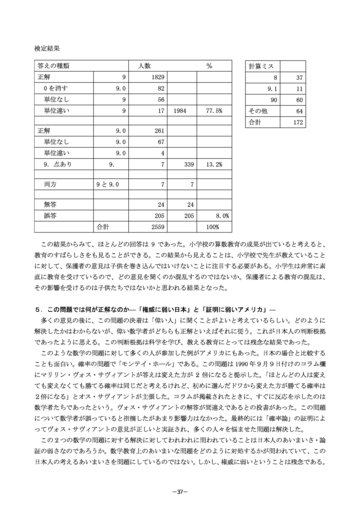
検定結果答えの種類正解 0 を消す単位なし単位違い正解単位なし単位違い 9．点あり両方無答誤答合計 9 9.0 9 9 9.0 9.0 9.0 9． 9 と 9.0 人数 1829 82 56 17 261 67 4 7 7 24 205 2559 339 7 24 205 8.0% 100% 13.2% 1984 77.5% その他合計％計算ミス 8 9.1 90 37 11 60 64 172 この結果からみて、ほとんどの回答は 9 であった。小学校の算数教育の成果が出ていると考えると、教育のすばらしさをも見ることができる。この結果から見えることは、小学校で先生が教えていることに対して、保護者の意見は子供を巻き込んではいけないことに注目する必要がある。小学生は非常に素直に教育を受けているので、どの意見を聞くのか混乱するのではないか。保護者による教育の混乱は、その影響を受けるのは子供たちではないかと思われる結果となった。５．この問題では何が正解なのか―「権威に弱い日本」と「証明に弱いアメリカ」― 多くの意見の後に、この問題の決着は「偉い人」に聞くことがよいと考えているらしい。どのように解決したかはわからないが、偉い数学者がどちらも正解といえばそれに従う。これが日本人の判断根拠であったように思える。この判断根拠は科学を学び、教える教育にとっては残念な結果であった。このような数学の問題に対して多くの人が参加した例がアメリカにもあった。日本の場合と比較することも面白い。確率の問題で「モンテイ・ホ―ル」である。この問題は 1990 年９月９日付けのコラム欄にマリリン・ヴォス・サヴィアントが答えは変えた方が 2 倍になると提示した。「ほとんどの人は変えても変えなくても勝てる確率は同じだと考えるけれど、初めに選んだドワから変えた方が勝てる確率は２倍になる」とオス・サヴィアントが主張した。コラムが掲載されたときに、すぐに反応を示したのは数学者たちであったという。ヴォス・サヴィアントの解答が間違えであるとの投書があった。この問題について数学者が誤っていると指摘したがあまり影響力はなかった。最終的には「確率論」の証明によってヴォス・サヴィアントの意見が正しいと実証され、多くの人々を悩ませた問題は解決した。この 2 つの数学の問題に対する解決に対してわれわれに問われていることは日本人のあいまいさ・論証の弱さなのであろうか。数学教育上のあいまいな問題をどのように対処するかが問われていて、この日本人の考えるあいまいさを問題にしているのではない。しかし、権威に弱いということは残念である。－37－
▲TOP

ページ： 41
今回のテレビでは「世界的数学者」として権威を強調していた感じがした。６．数学教育に残るあいまいなこと自然科学は実験結果が重要視される。実験によって求められたことが原理になり知識となって伝承されていく。数学では実験ができないのでこの問題の答えは何かをなんとかして決めたい。現在の教育ではどのような答えを信頼するのであろうか。科学の立場から今回の数学の問題を見たときに、何が問題なのか不思議に思うのではなかろうか。９か 9.0 かという問題ではなく、9.0 が正しいと思うのではなかろうか。数学教育においていろいろあいまいな問題がある。どのように答えるかはわからないことが多い。このような問題をほかにも挙げてみたらいろいろと挙げることができるであろう。思いつくままに挙げてみた。 (1)交換法則が成り立つか・単価ｓ円で個数ｔ個のときはｓ×ｔで交換は慣習として用いない・面積＝たて×横のときに「横×たて」でもよい？・定数×変数の順序で書くのが一般 (2)０で割ることの可能性・９÷０＝０になる回答が多い (3)有効数字は数学では教えない・3.1＋5.9 は 2 桁の有効数字を扱う・有効数字が 2 桁であれば 4.1＋5.9＝10 か 10.0 か？・位どりの０の重要性（３＋７＝１０か１）最後の桁の０を取る教育は 3＋7＝1 になる・電卓の計算結果はどこまで書くか (4)整数０１２は何桁の整数か (5)2 次方程式の解 x＝a、x＝b ・このカンマの意味は and か or か (6)1＝0.99・・・ (7)０は偶数か（小学校の教科書では偶数と明記） (8)凸多角形を扱う算数教育の中で星型の形は何角形かは逃げている。 (9)正方形は長方形の中に分類されるか？（正三角形は 2 等辺三角形か）この問題は教育という立場と学問という立場のどこに立って話をするかの問題と考えられる。新しい内容を扱う最初から正確さ、学問としての正しさの視点からのみ教育するときに、学ぶ側にとっては難しくて理解できないであろう。そのために多くの言葉があいまいになっている。このあいまいさをどの視点から問うかは厳密には考えられていない。今回の場合は 3.1+5.9 の答はないかという易しい問題でだれもが考えたくなった。教育的には小学校の 3 年生の教室でのやり取りを大切にすべきであった。生徒が先生の語る事柄を信頼して受け取ることができる雰囲気をつくることが必要である。そして、多くのことを学んだ後は学問としての正しさが要求される。その学問はその人それぞれの立場に立つことが大切であり、すべてを一つに決めることは必要ない。これからの社会では技術 (Technology）が重要視されるであろう。その Technology が打ち出す答えに対して何が正しいかを判断－38－
▲TOP

ページ： 42
するかが必要になる。判断できることはその人その人に要求されることであって、あいまいさのままで放置されることはない。この判断が要求されることは重要なことであり、今回のなにを正解にするかが決まらないということは、その人の数学観によることがあまりにも考えられなかった。数学教育を学校は大切な教科として教えていくが、その目標は学校での評価ではなく、これから常に学ぶ続ける生涯学習である。今回の話の中では、一人一人の生涯学習とは何か、何を目的にして学び続けるかが問われなかった。あいまいなことをきちんと解決できること、そして自ら考えることができる人を教育として、また学習として考えていく必要がある引用・参考文献 [1]日本数学検定協会算数問題検定 299 回９級 2017 [2]3.1＋5.9 の指導については小学校教科書 [3]テレビ朝日取材 2016.11.27 およびテレビ放送番組－39－
▲TOP

ページ： 43
【研究ノート】
▲TOP

ページ： 44
三乗和の公式の簡単な求め方学習数学研究所特別顧問一松信０．はじめに三乗数の和（略して三乗和とよぶ）の公式 3 １＋２3＋＋n 3 ＝  k 3 ＝  k＝１ n （n＋１） n   ２   ２ ……⑴ は有名でよく知られている。この公式は三角数Tn を活用すると，以下のように容易に示すことができる。簡単な注意だが，検定問題に出題されたこともあるので，この機会にまとめて３通りの証明を紹介する。１．準備―三角数の性質１＋２＋･･･＋n ＝Tn ＝ n （n＋１）２ ……⑵ は等差数列の和として，あるいは図形的にも容易に示される（三角数とよぶ）。補助定理として命題１ Tn－１＋Tn ＝ n 2 2 ……⑶ ……⑷ 命題２１＋３＋５＋･･･＋（２k －１）＝k きる。２．三乗和の公式―第１証明 ⑷は順次の奇数 k 個の和である。これらは⑵からも，あるいは図形的にも容易に証明で三角数の定義からTk －Tk－１＝k である。これと⑶（n を k とする）を掛けると 2 k3 ＝（Tk －Tk－１）（Tk ＋Tk－１）＝Tk 2 －Tk－１ ……⑸ 2 である。T0 ＝０，T1 ＝１により，⑸を k＝１から n まで加えれば，三乗数の和はTn となる。これは所要の式⑴である。▯ ３．三乗和の公式―第２証明１から始まる奇数の列を順次 k 個ごとに区切って，第 k ブロックC k とする。１｜３５｜７９ 11｜13 15 17 19｜21 ２Tk－１＋１＝ k 2－k＋１ 23 25 27 29｜･･･第 k ブロックの初項は，その前にTk－１個の奇数があるので ……⑹ －40－
▲TOP

ページ： 45
と表される。第 k ブロックの数の和は k 3 に等しい。これは等差数列の和だが，次のように考えてもよい。k が奇数なら中央項は k－１＝k2 ２ k－１組あるから総計 k 3 になる。 kが２ k 2－k ＋１＋２× であり，それをはさんで対称に和が２ k 2 になる組が偶数なら，両端の数の和が（ k 2－k ＋１）＋（ k 2－k ＋１＋２k －２）＝２ k 2 であり，同じ和の対が全体で k 組生じるから，やはり総計 k 3 である。２したがって最初から第 n ブロックまでの総和が，所要の三乗数の和に等しい。それは１から始めてTn 個の奇数の和であり，⑷によってTn 2 に等しい。▯ ４．三乗和の公式―第３証明次のような乗積表を考える。これを各行ごとに足せば，和は順次 Tn ，２Tn ，３Tn ，…，nTn であり，全体の和は Tn ×Tn ＝Tn 2 に等しい。他方左上から逆Ｌ字型に分けて足すと，最初のブロックは１だが，次は２＋４＋２＝２（１＋２＋１）＝２×２2＝２3 である。同様に第 k ブロックの和は k（１＋２＋…＋k ）＋k（１＋２＋…＋（k－１））＝kTk ＋kTk－１＝k× k 2 ＝ k 3 に等しい。したがって全体の和は三乗和 3 １＋２3＋＋n 3 に等しく，等式⑴を得る。▯ ５．むすび以上は一例にすぎない。これらはよく知られた結果だが，意外と工夫の余地があると感じたので，敢えて紹介した次第である。－41－
▲TOP

ページ： 46
数学カレンダーの作製は数学学習の普及を目指して数学学習研究所渡辺信１．数学が親子の対話の話題にちょっとした対話の中に「算数・数学」が話題にならないであろうか。家庭内における親子の話題が少なくなる傾向がある中で数学が話題になったら面白い。生涯学習としての数学学習は、学校の数学の試験結果ではないことが話題にならないであろうか。現在の数学学習が学校教育を超えて存在する場を作りたい。こんなことを思いながら、「数学カレンダー」が対話のきっかけになることを目指した。親子の対話の中で、今までは「算数の勉強をしなさい」とか「なんでこんなにできないの」とか、対話としては面白くなくなることが多かった。毎日カレンダーを見ながら問題を考え、家庭内で教えあえる環境を作りたい。今日からは「数学カレンダー」を見て、知っていることを教え合うことができたら面白い。親子の対話に、兄弟姉妹の間で、そして友達と「算数・数学」の話題旁をしたい。その話題作りに役立つ「数学カレンダー」作成をした。学校で習っていない算数・数学は問題を見ても全くわからない。わからないことを考えることはできないので、お互いに教えあうことを重視したい。親子の話で算数・数学の世界は広がったら、現在の学校教育とは違う数学学習の世界が広がるであろう。問題を解いて答えを出すだけではなく、算数・数学の話をお互いにすることによって数学の楽しさを体得したい。数学の考え方が世代を超えた「対話」によって広がる可能性がある。でも、学校教育は知識基盤を作ることに重要な役割を演じている。解けない問題に対して無理をする必要はない。できない問題、知らないことは後回しにしても良い。まだ習っていない問題がいっぱい並んでいることに疑問を感じるかもしれない。学校教育では学年制を敷いて、効率よく学ぶことを志しているために、上の学年の問題、数学を見ることができない。この「数学カレンダー」によって、全く新しい世界が見ることのできる体験は、数学の新しい世界を垣間見ることを可能にする。話をしながら考えていくことができたら、答えを出すだけではなく、数学の考え方をみんなで協力しながら身に付ける機会を作ることも可能になる２．「数学カレンダー」の問題について問題作成については、数学検定の問題を月曜日から金曜日まで、学年には関係なく並べてある。問題のグレードは参考のために、数学検定協会に従った。学校教育では 10 年ごとに学習指導要領が変わり、問題の程度が変化する。数学検定協会もこの学習指導要領に影響を受けつつも、身に付けてほしい数学知識を整理している。親子で学ぶ数学知識は学習指導要領の違いでだいぶ違っている可能性がある。親は学んでいても子供は知らないことや、ベクトル、行列など子供は知っていても親は全く名前も知らないこともあるであろう。お互いに協力して解決できればよい。また、休日には「考えたらできるかもしれない・聞いたこともない数学の言葉」が並んでいる。これは休日の問題を考えることによって、また一歩新しい数学の世界を知ってほしいと思うことによって作られた問題を並べた。学年によらずに考える楽しさを味わえることに重点を置いた。「考えてみたら、挑戦してみたら」数学知識がなくてもわかる－42－
▲TOP

ページ： 47
かもしれない問題が休日に並んでいる。意図的に学校教育には関係なく知っていてほしい事柄を意識的に並べてみた。数学は難しいというのではなく、数学を楽しんでほしい。月曜日から金曜日までの問題には「級」が付けてあります。次の表が問題の学年の目安になる。級５級４級３級準２級級なし目安となる学年中学生１年生程度を基準にしています中学生２年生程度を基準にしています中学生３年生程度を基準にしています高校１年生程度を基準にしています無学年の問題中学生が知っていることを含みます誰でも挑戦してください備考小学生が知っていることを含みます３．数学カレンダーの問題の答えについて答えは曜日毎にまとめて示した。答えが正解ならばよいというのではなく、対話することを大切にしたい。何か誰かと、この問題で話し合ったことがあったら「□の欄」にチェックしてみよう。できた問題には〇を付けるのも良いかもしれない。話し合った問題は正解が求まった以上に大きな力になる可能性がある。答えを求めるための過程は数学答案では「記述式」として重要であるが、このカレンダーはあくまでも対話を重視したい。問題を解く過程は示してはいない。答えだけであるがその答えに至る過程は「対話」である。４．カレンダー作成に当たって問題作成については「数学教育談話会の会員」で行った。この「数学カレンダー」作成についは、月曜日から金曜日までは、数学検定協会が作成・出題した問題を並べた。休日の問題については、新しい問題を作った。数学カレンダーを作ろうと思ったのは、数学学習を生涯学習の一環の中に位置付けたいとの思いが出発点であった。数学学習を生涯学習の中に位置づけることは、2010 年ごろから生涯学習としての数学学習についての研究から始まった。学校教育だけではなく家庭でも数学を学ぶことの可能性を追求したのが 2017 年であり、2018 年に数学カレンダーを作成する可能性が芽生えた。この生涯学習についての研究会は毎月一回行う数学教育談話会からの発想であった。この会のメンバーは次の通りである。渡辺信（数学学習研究所）、渡邊芳行（元 NTT エンジニア）、植野義明（東京工芸大学）、福田千枝子（帝京大学）、作本典子（元横浜市立高校教員）、青木孝子（東海大学）、岡田浩一（自営業）－43－
▲TOP

ページ： 49
公益財団法人日本数学検定協会が「記述式」を重んじる理由（2018 年 1 月 30 日）公益財団法人日本数学検定協会学習数学研究所当協会の行う「実用数学技能検定」（数学検定・算数検定）は、検定によって人をふるい分けるというものではありません。当協会は、いかに多くの「数学が好きな児童・生徒・学生・社会人を育てる」かが大切であると考えています。数学の問題を解くことを通して、数学を楽しむことができる機会を、検定という手法を用いて広くみなさまに提供しています。数学検定は、数学の知識をどれだけ覚えているかを問うものではありません。数学検定の正式名称は先に記したとおり実用数学技能検定で、社会や日常生活で数学がいかに使えるか、使われているかを、検定問題を通じて理解いただくことに重きを置いております。数学を理解し、使えるようになるということは、金融・情報・ＡＩ・工学・技術・流通・サービスなど、文系理系を問わず、さまざまな分野の発展に寄与する人材の育成につながります。また、数学的に考えることによって、他者との情報・意見交換が正確に行えるようになるということは、社会の中でとくに役立つ技能となります。当協会が、なぜ発足当初から記述式の答案を大切にしてきたかは、数学検定のあり方と直接かかわると同時に、数学という学問をいかに捉えるかに応えることとも関連します。数学的に考えることは人類にとって基本的な思考方法であり、この思考方法が存在することによって人類は社会を構築してきたといっても過言ではありません。数学の学びを通して、知識や技能を習得するだけでなく、それらを活用して問題を解決したり、新しい知識や技能を導き出したりする過程で、「考える」ことの質を高めていくことが大切です。このため、記述することは必要不可欠であると考えています。記述式を重んじる理由 (1)条件から結論を導くための筋道を記述することによって、情報を整理し、条件を導き出し、正確に伝える力を身に付けることができます。 (2)考えたこと、その過程や結果を記述することによって、考えがどこまで到達したかを確認でき、よりよい考えや説明の仕方を導くきっかけをみつけることができます。 (3)考え方を記述し振り返ることにより、数学的な考え方は一通りではないことが分かり、社会のさまざまな問題を解決する場合にも考え方は１つではないことが理解でき、物事を多面的に見る力を高めることができます。 (4)新しい知識や技能を導く過程で、その意味や手順を記述することによって、それらの知識・技能をよりよく習得することができます。 (5)自らの考えを記述して第三者に伝えることは、社会生活においても重要なことであり、数学の学びを通してその基礎的な技能を身につけることができます。以下に当協会が過去に出題した問題から２題（数学検定２級高等学校２年程度）を問題例として挙げます。問題例１は、日常生活の事象を数学的にとらえた問題です。解答例では１次不等式を使って解いていますが、方程式や１次関数のグラフを用いた解法も考えられます。記述式にすることで受検者のさまざまな考え方を捉えることができ、考え方がいろいろあり一通りでないこと知ることができます。記述式の出題により、正解に到達しなくても、途中の筋道が正しければ、部分点を付与することができます。問題例２は、社会の事象に関連した問題で、解答形式は短答式です。（２）では、新入社員をそれぞれの期待効果が最大の部署に配属することができないので、試行錯誤が必要です。その際、全体の期待効果が最大であることを確認するために数学的に考えることが必要となります。－44－
▲TOP

ページ： 50
問題例１（解答例）問題例２（解答）－45－
▲TOP

ページ： 51
飯高先生の数学講座 2013年から飯高茂先生（公益財団法人日本数学検定協会顧問・学習院大学名誉教授）による数学講座を年間４回のペースで開催している講座の内容は、高等学校の数学で扱う項目の延長線上にあるものや飯高先生の研究に関連するものを取り上げて、毎回オムニバス的に構成されている。受講者は小学生、中学生を含めて一般社会人まで幅広い。小中高校生にとっては学校の授業では味わえない数学に触れるよい機会になっている。一般社会人には数学の学び直しの場になっている。世界的数学者である飯高先生の講義を楽しみに参加している方も多い。第１回2013.08.21「不等式の力」第２回2013.09.17「射影幾何と２次曲線など」第３回2013.11.23「完全数とその一般化」第４回2014.03.01「代数学の基本定理をめぐって－ﾗﾌﾟﾗｽとｶﾞｳｽの知られざる戦い－」第５回2014.05.24「素数列の興味ある性質」第６回2014.08.30「集合論の不思議」第７回2014.11.24「ピタゴラスの定理と現代の数学」第８回2015.02.28「フェルマー素数５兄弟とオイラーのトシエント関数」第９回2015.05.23「整数の合同関係と分数」第10回2015.08.29「３次方程式の解の公式の解明」第11回2015.11.21「ダブルダイヤル数の数理」第12回2016.03.05「連分数と平方根への応用」第13回2016.05.21「49番目の完全数」第14回2016.09.03「楕円と離心率－惑星と彗星の運行－」第15回2016.11.19「ゲームより面白い半完全数」第16回2017.03.11「４元数とベクトルの外積」第17回2017.05.13「高校生の定義した新しい完全数」第18回2017.09.02「ピタゴラスからフェルマ」第19回2017.11.11「最大公約数と最小公倍数」第20回2018.03.03「ラッキーセブンの起源は循環小数」受講者数第１回 14 人第２回７人第３回 18 人第４回 18 人第５回 24 人第６回 25 人第７回 33 人第８回 28 人第９回第 10 回 18 人 28 人第 11 回第 12 回第 13 回第 14 回第 15 回第 16 回第 17 回第 18 回第 19 回第 20 回 16 人 36 人 26 人 19 人 26 人 18 人 17 人 18 人 18 人 19 人－46－
▲TOP

ページ： 52
文部科学省委託事業及び関連する事業－「高校生のための学びの基礎診断」（高等学校基礎学力テスト（仮称））－ ①「高等学校基礎学力テスト（仮称）」平成28年度試行調査平成28年8月10日付けで文部科学省により「高等学校基礎学力テスト（仮称）の問題の作成に関する調査研究事業委託要項」が公表され、「Ｂ．高等学校基礎学力テスト（仮称）の問題の作成に関する委託調査（数学科）」に応募した。平成28年 9月14日付けで委託が内定し、平成29年度以降の「プレテスト」実施のための試行調査用問題を作成した。高等学校段階（数学Ⅰ）の内容を中心とした標準レベル問題２セット、高等学校段階（数学Ⅰ）と義務教育段階の内容を半々に盛り込んだ基礎レベル問題２セット、及びＣＢＴ用問題を作成した。問題作成に関しては、検定問題品質委員の増田律子先生、田中紀子先生、塩澤友樹先生、小石沢勝之先生、竹内光悦先生、松嵜昭雄先生、及び小宮賢治評議員の協力を仰ぎ、ＣＢＴ用問題に関しては、ICTコネクト21会長の赤堀侃司先生に意見を頂いた。試行調査は、平成29年1月から3月にかけて、全国84の高等学校で実施された。 ②平成29年度施行調査・研究事業平成 29 年 9 月 20 日付けで文科省から「「高校生のための学びの基礎診断」に関する試行調査・研究事業委託要項」が公表された。「事業Ｃ．「高校生のための学びの基礎診断」に関する試行調査・研究事業（数学）」の企画提案書を提出したが、10 月 26 日付けで不採用の連絡があった。 ③平成28年度試行調査の結果検討会平成29年11月3日、平成28年度試行調査を実施した岡山県立勝間田高等学校の末廣教頭に実施結果を解説していただき、当協会が作成した問題を含めて検討した。問題ごとの正答率や得点を他社の測定ツールと比較し、当協会の作成した問題が基礎学力を測定するためのツールとして適切であることを確認した。 ④数検スコア総合診断【数Ⅰ・数Ａ】数学Ⅰ・数学Ａ修了後に数学ⅠＡ及び義務教育段階の数学の習得状態を総合的に診断するＣＢＴを、ＪＪＳプラスと共同開発している。このシステムを「高校生のための学びの基礎診断」の測定ツールとして認定申請する予定である。－47－
▲TOP

ページ： 53
数学検定の海外への普及学習数学研究所では海外への数学検定普及活動にも協力している。数学検定協会の普及活動とも協力しながら行った活動を記録しておく。（この記録は学習数学研究所と数学検定協会普及部の活動と重複する）数学検定のための海外出張報告年度 2015 年度 2016 年度期間 5 月 12 日～16 日 2 月 29 日～3 月 3 日国タイ (ＥＡＣＯＭＥ９) フィリッピン内容タイ数学検定最終打ち合わせフィリッピン検定 10 周年記念会検定実施中学校訪問 7 月 22 日～8 月 2 日ドイツ（ＩＣＭＥ１３） 2017 年度 10 月 15 日～18 日タイ数学検定紹介タイ数学検定との打ち合わせ 12 月 26 日～30 日ラオス（国際数学教育学会) 文部省へ数検紹介 ICME13 生涯学習について－48－
▲TOP

ページ： 54
学習支援 2017年度は小学校・中学校計９校で算数・数学の学習指導を行った。葛飾区立柴又小学校、葛飾区立中青戸小学校、葛飾区立葛飾小学校葛飾区立水元中学、葛飾区立中川中学、葛飾区立金町中学校、文京区立第八中学校、文京区立第十中学校、杉並区立松ノ木中学校イベントの実施小学生・中学生を対象としたイベントを開催し、算数・数学の楽しさを伝えた。 2017.03.29（水）学びのフェス 2017 春（科学技術館、主催：毎日新聞社、毎日小学生新聞）「数学マジックを作っちゃお!!」２進法を活用した数学マジックの制作を指導した。 2017.08.02（水）学びのフェス 2017 夏（科学技術館、主催：毎日新聞社、毎日小学生新聞）「数学マジックを作っちゃお!!」 2017.08.04（金）チャレンジセミナー in 光明（光明学園）「図形を用いた数学演習」 1 枚の紙から正二十面体を制作する方法を指導した。 2017.08 マスレチック・ランドパズルデー（主催：日本科学技術振興財団・科学技術館） 8/5･6 ミニ算数検定、8/9・10 円かき・立体を作ろう円かき：タブレットのディスプレイに円を描くと自動採点するソフトを用いた。立体：ストローとモールで正四面体・正八面体を制作した。 2017.09.22（金）算数トライアスロン（足立区立皿沼小学校）教員採用試験問題（数学）の分析各県の教員採用試験で出題された数学の問題と数学検定の問題を比較し、数学検定の何級に相当するかを分析した。教員採用試験（小学校教諭）：東京都、埼玉県・さいたま市、神奈川県・横浜市・川崎市・相模原市、千葉県・千葉市、大阪府・大阪市・堺市、愛知県、兵庫県教員採用試験（数学科）：東京都、神奈川県・横浜市・川崎市・相模原市、千葉県・千葉市－49－
▲TOP

ページ： 55
【会議報告】
▲TOP

ページ： 56
学習数学研究所運営会議場所：会議室（８人掛け）議事録日時：2018 年 2 月 6 日（火）16：30～18：30 出席者：清水、渡邉、中村、松本第１号議案運営会議の開催の件公益財団法人日本数学検定協会学習数学研究所運営規程第 10 条により運営会議を開く。毎年２月～３月に定例の運営会議を開催することが提案され、審議の結果、全会一致で承認された。この他、必要に応じて臨時の運営会議を開催することが提案され、審議の結果、全会一致で承認された。第２号議案学習数学研究所紀要の件学習数学研究所紀要を発行することが提案され、審議の結果、全会一致で承認された。 2018 年度中に創刊号（平成 29 年度版）を発行し、その後、年度版を年１回発行する。体裁はＡ４判 10.5 ポイントで、巻頭言、論説、報告、ニュースレター、編集後記等を掲載する。研究所顧問、検定問題品質委員にも執筆を依頼する予定である。印刷部数は 100 部～200 部程度の予定。事業報告１．学術研究機関指定の件 2017年８月31日付けで文部科学省から科学研究費補助金取扱規程に規定する研究機関としての指定を受けた。 e-Rad（府省共通研究開発管理システム）に研究者の登録をした。清水静海（所長）、渡邉信（研究員）、松本精一（所長代理）、中村力（上席研究員）、松嵜昭雄（特任研究員）、塩澤友樹（特任研究員）事業報告２．検定問題品質会議の件 2018 年２月 11 日（日）全体会・分科会（幼小中部会・高大部会）及び情報交換会を開催する。全体会では「記述について」の講演を、羽中田委員、澤田委員、塩澤委員に依頼した。事業報告３．高等学校基礎学力テスト（仮称）に関する調査研究事業の結果検討の件 2016年、文部科学省「高等学校基礎学力テスト（仮称）の問題の作成に関する調査研究事業」委託調査（数学科）を受託し、平成29年度以降の「プレテスト」実施のための試行調査用問題を作成した。 2017年11月3日、平成28年度試行調査を実施した岡山県立勝間田高等学校の末廣教頭に実施結果を解説していただき、当協会が作成した問題を含めて検討した。－50－
▲TOP

ページ： 57
JJS と共同開発している数検スコア診断テスト（ＣＢＴ）を「高校生のための学びの基礎診断（仮称）」の測定ツールとして申請する予定である。事業報告４．検定問題等検討会の件 2017 年 11 月から毎月１回検定問題等検討会を開催し、検定問題を中心として、大学入学共通テストプレテストの問題、数学教育等について検討している。事業報告５．数学講座の件 2013 年８月から飯高茂先生（学習院大学名誉教授・公益財団法人日本数学検定協会顧問）の数学講座を年間４回実施している。数学の生涯学習をする貴重な講座であるとともに、才能ある児童・生徒のための高度な数学学習の場として活用されている。事業報告６．算数・数学イベントの件小学生・中学生を対象としたイベントを開催し、算数・数学の楽しさを伝えた。 2017.08.02 学びのフェス 2017 夏（科学技術館、主催：毎日新聞社、毎日小学生新聞） 2017.08.04 チャレンジセミナー in 光明（光明学園） 2017.08 マスレチック・ランドパズルデー（主催：日本科学技術振興財団・科学技術館） 2017.09.22 算数トライアスロン（足立区立皿沼小学校）事業報告７．学習支援の件現在、小学校・中学校合わせて９校程度で学習支援を行っている。目的は、算数・数学への興味関心を高める、検定実施前の数学力向上等が挙げられる。現在実施している講座に関しては、要請があれば今後も続けていく。事業報告８．出版の件改訂版「ためせ実力！めざせ 1 級！数学検定 1 級実践演習（第２版）」（森北出版）の原稿を執筆している。－51－
▲TOP

ページ： 58
検定問題品質会議 2018.02.11 ・全体会（出席者 42 人：外部委員 16 人、役員・職員 21 人、タイ数学検定協会５人）講演：「記述」について羽中田彩記子（日本女子大学）、澤田章（葛飾区立亀有中学校）塩澤友樹（東京都立白鴎高等学校・附属中学校）・分科会（出席者 42 人）小中部会、高大部会に分かれて、委員の先生方が作成した問題を検討した。・情報交換会（出席者 37 人）・検定問題品質委員島田功小学校中村真也中学校高等学校毛利哲松浦昭洋大学渡辺美智子その他協会役員等根上生也松本精一稲葉大樹協会職員三上佳津江稲田敬亮加藤聖治田中麻由子藤原綾依渡辺拓馬黒田裕美橋本和枝加藤龍平飯高茂中村力阿部加奈子杉本勝秀大村有紀水原柳一郎山口哲穂積悠樹上林航大迫ちあき一松信竹内光悦難波俊樹甘利俊一深澤弘美呉我春尚清水静海田澤義彦北澤正樹渡邉信小宮賢治藤田岳彦末廣聡牧下英世吉川厚大谷信一松嵜昭雄増田律子高橋進野島泰一後藤宣孝古宇田大介川上貴澤田章田中紀子塩澤友樹小石沢勝之羽中田彩記子白井一之小坂裕皇菅野宏隆－52－
▲TOP

ページ： 59
検定問題等検討会 2017.11.22 （第１回）「３級２次検定正答率が低い問題について」 304 回（7/8）、305 回（7/23）、306 回（8/26）の３級２次検定において、中学校第３学年の範囲で正答達成率が低かった問題を抽出し、過去の類似問題と比較して、出題方法、実施時期等影響がありそうな項目について検討した。参加者：高田、渡邉、中村、杉本、松本 2017.12.20 （第２回）「３級２次検定論述式問題と短答式問題についての比較」３級２次検定で出題された論述式問題と短答式問題の比較をし、記述式について意見交換をした。三平方の定理と関数 y＝ax2 について、設問が似ている問題を取り上げた。論述式でも短答式でも正答達成率に差はないようであったが、論述式で出題することによって、受検者が考えをまとめる訓練になると考えられる。参加者：高田、渡邉、中村、松本、穂積、藤原、稲田 2018.01.24 （第３回）「記述式について」「公益財団法人日本数学検定協会が「記述式」を重んじる理由」及び大学入学共通テスト試行調査問題（数学ⅠＡ第１問．２次関数）を参考資料として、記述式について意見交換をした。解法を誘導するような設問は、自由な思考を妨げるという意見や、公正で正確な採点をする上で必要である、最善の解法を誘導するのであればあり得る等様々な意見が出た。参加者：渡邉、中村、松本、杉本、水原、黒田 2018.02.21（第４回）「大学入試センター試験数学ⅠＡの問題の検討」大学入試センター試験数学ⅠＡの問題を検討した。各問題の解法、ポイント、数学検定の問題との比較、統計の問題の数学検定での出題の仕方等について意見交換した。担当：第１問（渡邉先生）、第２問（上林）、第３問（中村）、第４問（藤原）、第５問（水原）参加者：渡邉、中村、松本、水原、上林、藤原 2018.03.14（第５回）「高等学校新学習指導要領について」高等学校の新学習指導要領について意見交換をした。とくに、数学Ｂから数学Ｃへ移行したベクトルや扱いが縮小した「整数」、現在の指導要領と同様ほとんど扱われていない行列と、数学検定との関連について意見があった。参加者：渡邉、中村、松本、穂積、稲葉、渡辺拓－53－
▲TOP

ページ： 60
【規程類】
▲TOP

ページ： 61
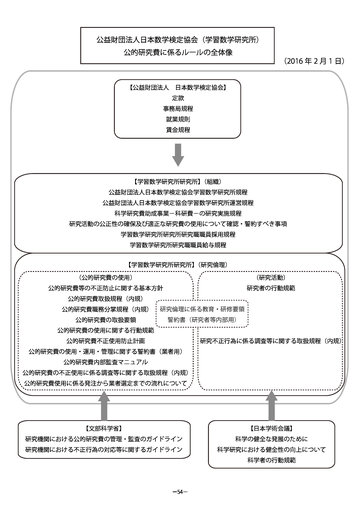
公益財団法人日本数学検定協会（学習数学研究所）公的研究費に係るルールの全体像（2016 年 2 月 1 日）【公益財団法人日本数学検定協会】定款事務局規程就業規則賃金規程【学習数学研究所研究所】（組織）公益財団法人日本数学検定協会学習数学研究所規程公益財団法人日本数学検定協会学習数学研究所運営規程科学研究費助成事業−科研費−の研究実施規程研究活動の公正性の確保及び適正な研究費の使用について確認・誓約すべき事項学習数学研究所研究所研究職職員採用規程学習数学研究所研究職職員給与規程【学習数学研究所研究所】（研究倫理）（公的研究費の使用）公的研究費等の不正防止に関する基本方針公的研究費取扱規程（内規）公的研究費職務分掌規程（内規）公的研究費の取扱要領公的研究費の使用に関する行動規範公的研究費不正使用防止計画公的研究費の使用・運用・管理に関する誓約書（業者用）公的研究費内部監査マニュアル公的研究費の不正使用に係る調査等に関する取扱規程（内規）公的研究費使用に係る発注から業者選定までの流れについて研究不正行為に係る調査等に関する取扱規程（内規）研究倫理に係る教育・研修要領誓約書（研究者等内部用）（研究活動）研究者の行動規範【文部科学省】研究機関における公的研究費の管理・監査のガイドライン研究機関における不正行為の対応等に関するガイドライン【日本学術会議】科学の健全な発展のために科学研究における健全性の向上について科学者の行動規範ー54－
▲TOP

ページ： 62
公益財団法人日本数学検定協会（前文）学習数学研究所規程(*) 公益財団法人日本数学検定協会（以下、「本協会」という）は、本協会事務局規程第２条に基づき、事務局に学習数学研究所を設置する。（趣旨）第１条この規程は、学習数学研究所（以下、「研究所」という。）に関して定めたものである。（目的）第２条研究所は、本協会における研究の基盤を担い、実用数学技能検定（数学検定・算数検定）を中心とした研究及び調査を行い、数学の生涯学習の進歩発展に寄与することを目的とする。（事業）第３条研究所は、第２条の目的を達成するために次の事業を行う。（１）数学の生涯学習に関する研究（２）検定に関する研究（３）算数教育及び数学教育に関する研究（４）研究会、講演会等の開催（５）紀要、年報、叢書等の刊行（６）その他必要な事業（組織・運営）第４条研究所の組織・運営等に関しては別に定める「公益財団法人日本数学検定協会学習数学研究所運営規程」による。（職員）第５条研究所の職員は、研究職職員及び事務職職員とする。（採用）第６条研究職職員の採用に関する事項については、別に定める「公益財団法人日本数学検定協会学習数学研究所研究職職員採用規程」による。２事務職職員の採用に関する事項については、本協会就業規則を準用する。 (*)平成28年2月1日制定－55－
▲TOP

ページ： 63
（給与）第７条研究職職員の給与に関する事項については、別に定める「公益財団法人日本数学検定協会学習数学研究所研究職職員給与規程」による。２事務職職員の給与に関する事項については、本協会賃金規程を準用する。（準用）第８条この規程に定める事項以外の事項については、本協会の規程類を準用する。（雑則）第９条この規程に定めるもののほか、規程の施行に関し、必要な事項は理事会の決議を経て定める。（規程の改廃）第10条この規程の改廃は、理事会の決議を経て行う。附則この規程は、平成 28 年２月１日から施行する。－56－
▲TOP

ページ： 64
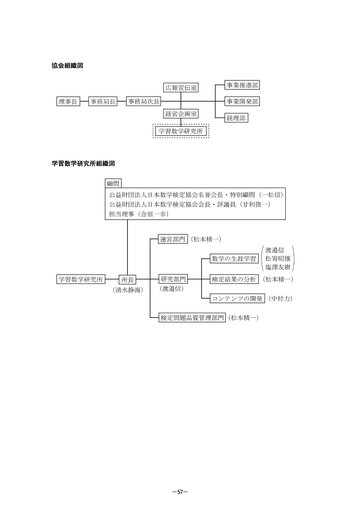
協会組織図学習数学研究所組織図－57－
▲TOP

ページ： 65
公益財団法人日本数学検定協会学習数学研究所運営規程(*) （趣旨）第１条この規程は、公益財団法人日本数学検定協会（以下「本協会」という。）学習数学研究所規程第４条の規定に基づき、学習数学研究所（以下「研究所」という。）の組織・運営等に関し必要な事項を定めるものとする。（目的）第２条研究所は、公益財団法人日本数学検定協会（以下「本協会」という。）における研究の基盤を担い、実用数学技能検定（数学検定・算数検定）を中心とした研究及び調査を行い、数学の生涯学習の進歩発展に寄与することを目的とする。（事業）第３条研究所は、第２条の目的を達成するため、次の事業を行う。（１）数学の生涯学習に関する研究（２）検定に関する研究（３）算数教育及び数学教育に関する研究（４）研究会、講演会等の開催（５）紀要、年報、叢書等の刊行（６）その他必要な事業（組織）第４条研究所に、運営部門、研究部門及び検定問題品質管理部門を置く。（職員）第５条研究所の職員は、本協会の職員のうちから本協会事務局規程第５条２の規定に基づき任命される。２研究所の職員は、研究職職員及び事務職職員とする。３研究所は、必要に応じて、本協会の検定問題品質委員ならびに本協会と協力関係にある者を第３条に規定する事業に参加させることができる。（研究職の構成）第６条研究職職員の職階は、上席研究員、主任研究員、研究員、特任研究員とする。２上席研究員、主任研究員、研究員は、それぞれ本協会の部長、マネジャー、チーフに相当するものとする。（研究所長）第７条研究所長は、理事長が任命する。２研究所長は、研究所の業務を統括し、研究所を代表する。 (*)平成 28 年 2 月 1 日制定－58－
▲TOP

ページ： 66
（任期）第８条研究所長の任期は、２年とする。２研究所長は、再任されることができる。３研究所長は、本協会の部長と同等の待遇を有するものとする。（所長代理）第９条所長代理は、理事長が任命する。２所長代理は、研究所長を補佐する。３所長代理は、本協会の部長と同等の待遇を有するものとする。（運営会議）第 10 条次に掲げる事項について審議するため、運営会議を置く。（１）第３条に規定する事業及びその事業計画に関する事項（２）その他運営に関する事項２運営会議は、研究所長、所長代理及び各部門の代表をもって構成する。３運営会議は、研究所長が招集し、その議長となる。４運営会議は、構成員の半数以上が出席しなければ、会議を開き議決することができない。５運営会議の議事は、出席した構成員の過半数でこれを決し、可否同数のときは、議長がこれを決する。（申請）第11条第３条に規定する研究を担当しようとする者は、研究申請書に必要事項を記入し、研究所長に提出しなければならない。（研究者）第12条前条の規定により、研究申請書を提出し、研究を認められた者（以下「研究者」という。）は、研究費の助成を受けることができる。２研究者は、当該年度の研究実施計画書を定められた期日までに、研究所長に提出しなければならない。３研究者は、研究費の使用状況報告書を当該年度末日までに、研究所長に提出しなければならない。４研究者は、研究終了後、研究成果を研究所長に報告しなければならない。（報告）第13条研究所長は、研究者の研究事項及び研究費について理事長に報告しなければならない。（研究成果の報告）－59－
▲TOP

ページ： 67
第14条研究所は、研究者の研究成果を公表するため、紀要、年報、叢書等を刊行する。２研究所は、研究部門の職員以外の者の紀要への投稿を認めることができる。（事業報告）第15条研究所長は、毎年度第３条に規定する事業について理事長に報告しなければならない。（図書・資料・機器備品）第16条研究者が研究のために収集した図書、資料及び機器備品は、すべて本協会に帰属するものとする。（事務）第17条研究所に関わる申請事務は、研究所が行う。２研究所に関わる経理事務は、本協会経理部が行う。（経費）第18条研究所の経費は、本協会予算によって定められた経費をもって支弁する。（雑則）第19条この規程に定めるもののほか、規程の施行に関し、必要な事項は理事会の決議を経て定める。（規程の改廃）第20条この規程の改廃は、理事会の決議を経て行う。附則この規程は、平成 28 年２月１日から施行する。－60－
▲TOP

ページ： 68
研究者の行動規範 (*) 研究者が当然備えるべきものである倫理を、公益財団法人日本数学検定協会（学習数学研究所）における研究者の行動規範として作成した。この行動規範は、「科学者の行動規範」（平成２５年１月２５日日本学術会議）に準拠して作成したものである。なお、本行動規範における「研究者」とは、「公益財団法人日本数学検定協会（学習数学研究所）運営規程」に定める研究職職員を意味する。 Ⅰ．研究者の責務（研究者の基本的責任）１研究者は、自らが生み出す専門知識や技術の質を担保する責任を有し、さらに自らの専門知識、技術、経験を生かして、人類の健康と福祉、社会の安全と安寧、そして地球環境の持続性に貢献するという責任を有する。（研究者の姿勢）２研究者は、常に正直、誠実に判断、行動し、自らの専門知識・能力・技芸の維持向上に努め、科学研究によって生み出される知の正確さや正当性を科学的に示す最善の努力を払う。（社会の中の研究者）３研究者は、科学の自律性が社会からの信頼と負託の上に成り立つことを自覚し、科学・技術と社会・自然環境の関係を広い視野から理解し、適切に行動する。（社会的期待に応える研究）４研究者は、社会が抱く真理の解明や様々な課題の達成へ向けた期待に応える責務を有する。研究環境の整備や研究の実施に供される研究資金の使用にあたっては、そうした広く社会的な期待が存在することを常に自覚する。（説明と公開）５研究者は、自らが携わる研究の意義と役割を公開して積極的に説明し、その研究が人間、社会、環境に及ぼし得る影響や起こし得る変化を評価し、その結果を中立性・客観性をもって公表するとともに、社会との建設的な対話を築くように努める。 (*)平成 29 年 9 月 1 日制定－61－
▲TOP

ページ： 69
（科学研究の利用の両義性）６研究者は、自らの研究の成果が、研究者自身の意図に反して、破壊的行為に悪用される可能性もあることを認識し、研究の実施、成果の公表にあたっては、社会に許容される適切な手段と方法を選択する。 Ⅱ．公正な研究（研究活動）７研究者は、自らの研究の立案・計画・申請・実施・報告などの過程において、本規範の趣旨に沿って誠実に行動する。研究者は研究成果を論文などで公表することで、各自が果たした役割に応じて功績の認知を得るとともに責任を負わなければならない。研究・調査データの記録保存や厳正な取扱いを徹底し、ねつ造、改ざん、盗用などの不正行為を為さず、また加担しない。（研究環境の整備及び教育啓発の徹底）８研究者は、責任ある研究の実施と不正行為の防止を可能にする公正な環境の確立・維持も自らの重要な責務であることを自覚し、科学者コミュニティおよび自らの所属組織の研究環境の質的向上、ならびに不正行為抑止の教育啓発に継続的に取り組む。また、これを達成するために社会の理解と協力が得られるよう努める。（研究対象などへの配慮）９研究者は、研究への協力者の人格、人権を尊重し、福利に配慮する。動物などに対しては、真摯な態度でこれを扱う。（他者との関係）１０研究者は、他者の成果を適切に批判すると同時に、自らの研究に対する批判には謙虚に耳を傾け、誠実な態度で意見を交える。他者の知的成果などの業績を正当に評価し、名誉や知的財産権を尊重する。また、科学者コミュニティ、とくに自らの専門領域における研究者相互の評価に積極的に参加する。 Ⅲ．社会の中の科学（社会との対話）１１研究者は、社会と科学者コミュニティとのより良い相互理解のために、市民との対話と交流に積極的に参加する。また、社会の様々な課題の解決と福祉の実現を図るために、政策立案･決定者に対して政策形成に有効な科学的助言の提供に努める。その際、研究－62－
▲TOP

ページ： 70
者の合意に基づく助言をめざし、意見の相違が存在するときはこれを解りやすく説明する。（科学的助言）１２研究者は、公共の福祉に資することを目的として研究活動を行い、客観的で科学的な根拠に基づく公正な助言を行う。その際、研究者の発言が世論および政策形成に対して与える影響の重大さと責任を自覚し、権威を濫用しない。また、科学的助言の質の確保に最大限努め、同時に科学的知見に係る不確実性及び見解の多様性について明確に説明する。（政策立案･決定者に対する科学的助言）１３研究者は、政策立案･決定者に対して科学的助言を行う際には、科学的知見が政策形成の過程において十分に尊重されるべきものであるが、政策決定の唯一の判断根拠ではないことを認識する。科学者コミュニティの助言とは異なる政策決定がなされた場合、必要に応じて政策立案･決定者に社会への説明を要請する。 Ⅳ．法令の遵守など（法令の遵守）１４研究者は、研究の実施、研究費の使用等にあたっては、法令や関係規則を遵守する。（差別の排除）１５研究者は、研究・教育・学会活動において、人種、ジェンダー、地位、思想・信条、宗教などによって個人を差別せず、科学的方法に基づき公平に対応して、個人の自由と人格を尊重する。（利益相反）１６研究者は、自らの研究、審査、評価、判断、科学的助言などにおいて、個人と組織、あるいは異なる組織間の利益の衝突に十分に注意を払い、公共性に配慮しつつ適切に対応する。附則（施行期日）この行動規範は、平成２９年９月１日から施行する。－63－
▲TOP

ページ： 71
編集後記公益財団法人日本数学検定協会学習数学研究所が設立されてから２年がたちました。ここに、研究所紀要を発行することとなり、研究論文、研究ノート、報告、会議報告、研究所の規程類等で構成しました。研究所顧問の先生方からはお祝いのお言葉をいただきました。また、検定問題品質委員の先生方にもご助力いただきました。創刊号（第１巻）を発行するにあたり、ご協力いただいた方々に心よりお礼申し上げます。（松本精一）編集委員島田功清水静海中村力羽中田彩記子松嵜昭雄松本精一渡邉信学習数学研究所紀要創刊号（第１巻）発行日 2018 年 3 月 31 日編集発行公益財団法人日本数学検定協会学習数学研究所所長清水静海〒110-0005 東京都台東区上野 5-1-1 TEL 03-5812-8340 FAX 03-5812-8346 印刷所サイトー印刷株式会社－64－
▲TOP

学習数学研究紀要 創刊号（第1巻）

学習数学研究紀要　創刊号（第1巻）