学習数学研究紀要 創刊号（第1巻）
- ページ： 40
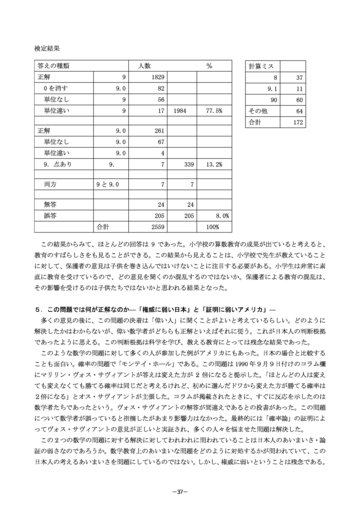
- 検定結果 答えの種類 正解 0 を消す 単位なし 単位違い 正解 単位なし 単位違い 9．点あり 両方 無答 誤答 合計 9 9.0 9 9 9.0 9.0 9.0 9． 9 と 9.0 人数 1829 82 56 17 261 67 4 7 7 24 205 2559 339 7 24 205 8.0% 100% 13.2% 1984 77.5% その他 合計 ％ 計算ミス 8 9.1 90 37 11 60 64 172
この結果からみて、ほとんどの回答は 9 であった。小学校の算数教育の成果が出ていると考えると、 教育のすばらしさをも見ることができる。この結果から見えることは、小学校で先生が教えていること に対して、保護者の意見は子供を巻き込んではいけないことに注目する必要がある。小学生は非常に素 直に教育を受けているので、どの意見を聞くのか混乱するのではないか。保護者による教育の混乱は、 その影響を受けるのは子供たちではないかと思われる結果となった。 ５．この問題では何が正解なのか―「権威に弱い日本」と「証明に弱いアメリカ」― 多くの意見の後に、この問題の決着は「偉い人」に聞くことがよいと考えているらしい。どのように 解決したかはわからないが、偉い数学者がどちらも正解といえばそれに従う。これが日本人の判断根拠 であったように思える。この判断根拠は科学を学び、教える教育にとっては残念な結果であった。 このような数学の問題に対して多くの人が参加した例がアメリカにもあった。日本の場合と比較する ことも面白い。確率の問題で「モンテイ・ホ―ル」である。この問題は 1990 年９月９日付けのコラム欄 にマリリン・ヴォス・サヴィアントが答えは変えた方が 2 倍になると提示した。 「ほとんどの人は変え ても変えなくても勝てる確率は同じだと考えるけれど、初めに選んだドワから変えた方が勝てる確率は ２倍になる」とオス・サヴィアントが主張した。コラムが掲載されたときに、すぐに反応を示したのは 数学者たちであったという。ヴォス・サヴィアントの解答が間違えであるとの投書があった。この問題 について数学者が誤っていると指摘したがあまり影響力はなかった。最終的には「確率論」の証明によ ってヴォス・サヴィアントの意見が正しいと実証され、多くの人々を悩ませた問題は解決した。 この 2 つの数学の問題に対する解決に対してわれわれに問われていることは日本人のあいまいさ・論 証の弱さなのであろうか。数学教育上のあいまいな問題をどのように対処するかが問われていて、この 日本人の考えるあいまいさを問題にしているのではない。 しかし、 権威に弱いということは残念である。
－37－
- ▲TOP
