 学習数学研究紀要 創刊号(第2巻)
学習数学研究紀要 創刊号(第2巻)

- ページ: 1
- 学習数学研究紀要
第2巻
公益財団法人 日本数学検定協会 学習数学研究所
�
- ▲TOP

- ページ: 2
- 学習数学研究紀要 第2巻
目次 1 2
巻頭言………………………………………………………………………………………… 髙田 忍 数学検定・算数検定への期待……………………………………………………………… 島田 功
個々の学びの改善に向けた数学検定・算数検定への期待……………………………… 塩澤 友樹 3 【研究論文】 高校理科における数学活用調査………………………………………………………… 中村 力 除法を使って解く問題に見られる誤答 -算数検定の記述式問題の答案の分析を通して-……………………………… 松本 精一 9 数検答案から見た数学教育の問題点 -公式に頼る数学教育から数学を楽しむ数学検定へ-………………………… 【研究ノート】 2次行列の累乗について………………………………………………………………… 一松 信 直線上の点 E で AEn+BEnを最小とする点 E の位置変化……………………………… 渡辺 信 29 33 渡辺 信 22 4
大学に向けた記述式の提案……………………………………………………………… 松本 精一 36 【報告】 飯高先生の数学講座……………………………………………………………………………………… 42 研究機関の指定について………………………………………………………………………………… 44 文部科学省認定「高校生のための学びの基礎診断」測定ツール…………………………………… 45 免許状更新講習…………………………………………………………………………………………… 46 数学検定の海外への普及………………………………………………………………………………… 48 出版………………………………………………………………………………………………………… 49 学習支援…………………………………………………………………………………………………… 49 イベントの実施…………………………………………………………………………………………… 50 【会議報告】 学習数学研究所 運営会議議事録……………………………………………………………………… 51 検定問題品質会議………………………………………………………………………………………… 53 検定問題等検討会………………………………………………………………………………………… 54 (資料) 問題検討会………………………………………………………………………………………………… 68 編集後記……………………………………………………………………………………………………… 69 【付録】 全体関連マップ:高校理科と数学の定性的依存関係 1.高校物理 俯瞰チャート 2.高校化学 俯瞰チャート 3.高校生物 俯瞰チャート 4.高校地学 俯瞰チャート
�
- ▲TOP

- ページ: 3
- 巻頭言 公益財団法人 日本数学検定協会 専務理事 髙田 忍
『学習』について、広辞苑には「①まなびならうこと②経験によって新しい知識・技能・ 態度・行動傾向・認知様式などを習得すること、およびそのための活動。 」という解説文が 記されています。 名は体を表すということわざにもあるとおり、名称を適切に捉えるということは大変重 要です。それでは「学習数学研究所」という名称に注目して、そこに込められた想いなどに ついて考えてみましょう。 「数学研究所」 という名称であれば、 単純に高度な数学を研究する機関ということが直感 的に理解できると思いますが、名称の先頭に「学習」ということばがつくことによって、そ の意味合いは変わってきます。そこで「学習数学研究所」の目的を見ておきましょう。 「学習数学研究所は、当協会における研究の基盤を担い、実用数学技能検定(数学検定・ 算数検定) を中心とした研究及び調査を行い、 数学の生涯学習の進歩発展に寄与することを 目的として、2016 年 2 月に設置された研究機関です。 」と、記されています。 「学習数学研究所」 では単に数学を学び習うことを研究するということだけではなく、 数 学に関する知識や技能などを習得する方法やそのための活動に至るまで大変広い領域につ いても研究していくということにつながります。特にその活動方法や活動する環境づくり はこれからの日本を考える上でとても価値のある取り組みです。 これまで、 数学については学校教育を中心に学習方法などが研究されてきました。 しかし、 これからは生涯学習という大きな枠組みの中で数学をいかにして学ぶかについて考えてい かなければなりません。そして、日本の生涯学習には検定制度がとても合っています。 当研究所の母体となる日本数学検定協会では、実用数学技能検定「数検」という検定制度 を提供していますが、毎年幼児からシニアの方まで幅広い世代の方が受検しています。 そもそも検定制度は華道や茶道といった道の精神を高めるような活動に似ています。検 定制度はよく資格制度に間違われてしまうのですが、 根本的には全く異なります。 資格制度 はある職業や企業に入るために使われるもので、 その目的はほぼ定められています。 しかし、 検定制度は自分の力を測るもので、その目的は個人個人で異なります。もちろん、大学に入 学するためだったり、企業に就職するためだったりと資格制度と同じように1つの目的で 受検する人もいますが、 検定取得を趣味としていたり、 脳の活性化のためだったりと受検の 目的はさまざまです。こうした状況に鑑みると学習数学研究所は数学を学習するすべての 人たちの活動に目を向け、 その学習環境を整備していかなければなりません。 人の数だけそ の目的は違うために、それぞれに対応した学習環境を整えていくことはとても難しいこと ではありますが、1つ1つ着実に研究していくことが大きな取り組みにつながっていくと 信じています。 数学を学習する方には是非とも多くのご意見ご要望などお寄せいただき、これからの研 究所を支えていただきますよう、心よりお願い申し上げます。
- 1 -
�
- ▲TOP

- ページ: 4
- 数学検定・算数検定への期待
公益財団法人 日本数学検定協会 検定問題品質委員 島田 功(*)
1988 年に数学の検定制度が開発され、2018 年に 30 周年を迎えました。1992 年に実施し た第1回数学検定の受検者数は、およそ 5500 人でした。それが 2018 年には、受験者数が 376000 人になり、 多くの方に数学検定・算数検定が認知され支持されるようになりました。 私は第 1 回から算数検定の問題作成に関わり、スタート時は、水道橋の「神田パンセ」を 会場に 3 人の先生方で作成しておりました。 その当時、 「算数と音楽との関係」 の問題や 「算 数と体育との関係」の問題を作ったことを覚えております。このような他教科との関わり の問題は、文部科学省の全国学力・学習状況調査の活用問題の中の他教科における算数活 用問題を先取りした問題とも言えます。 また、数学検定・算数検定は、今では日本だけではなく、フィリピンやカンボジアやタ イでも実施されるようになり、国際的な広がりを見せるようになりました。このことは、 数学検定・算数検定の国際化が進んでいる証左です。実に隔世の感を覚えます。 更には、日本数学検定協会の設立の目的には「信頼性と有用性が高く、学習指針として 広く認められる数学に関する検定事業を実施し、得られた知見を社会に還元することを通 じて、世界中の人々の生涯に渡る数学への興味喚起と数学力の向上に貢献する」とあるよ うに数学検定・算数検定は生涯学習としての役割を持ち合わせております。受検者層は、 子どもから大人まで幅広い層から成り立ち、その目的も多様性を示しています。 こうした数学検定・算数検定の生涯学習としての役割を日本数学教育学会の全国大会や 春期大会で日本数学検定協会の松本氏や渡辺氏等により発表されております。その結果、 日本数学教育学会の会員も数学検定・算数検定の生涯学習としての役割に注目を集めるよ うになりました。そしてこれからも生涯学習としての数学検定・算数検定の役割の重要性 は益々高まりを見せることになると思います。 数学検定・算数検定の今後の更なる発展を期待しております。
(*)日本体育大学大学院教育学研究科教授・教育学博士
- 2 -
�
- ▲TOP

- ページ: 5
- 個々の学びの改善に向けた数学検定・算数検定への期待
学習数学研究所 特任研究員 塩澤 友樹(*) 「3a-a=3」 。 「2 つの底角が等しい三角形は、二等辺三角形である」 。これらは、中学校 の授業で出会う代表的な 2 つの誤答である。前者は中学 1 年生の文字式の計算でよくある 誤りである。生徒は「ひくは取るだから、3a から a を取ればよい」と解釈し、解答したと 推察される。一方、後者は議論の余地が残るが、中学校の教科書では、二等辺三角形の底辺 の両端の角を「底角」と定義する。そのため、二等辺三角形と分からない段階では、 「2 つ の角が等しい三角形は、二等辺三角形である」と表現する。生徒は何となく回答したと答え るかもしれないが、この命題を通して、証明の学習における言葉の大切さ、論理的に考える ことの大切さを実感する。 中学生の授業を受け持った際、 毎年これらに戸惑う生徒がいる一 方、授業で取り上げた際に盛り上がる内容でもあった。私は初任者の頃、これらの反応を予 想することはできなかった。しかし、毎年、授業を受け持つ中で同じ内容でつまずく生徒に 出会い、逆にクラス全体で共有することで、生徒のつまずきを減らすことができた。このよ うに考えると、数学検定・算数検定にも同様の効果が期待できる。 現在の社会は、IT 機器の普及や AI(人工知能) 、ビッグデータ等の社会実装により、新た な市場が開拓され、 「第 4 次産業革命」を迎えている( [1] ) 。数学の重要性が増す中で、算 数・数学に関する素養を身に付けることはより一層重要になっている。 一方、 社会が多様化・ 複雑化するからこそ、1 人 1 人が自己の学びを客観的に評価すること、さらには典型的な誤 答に気付き、より深く自己の学びを把握し、改善できる学習環境を整える必要がある。例え ば、受検者個人として、数学検定・算数検定の合否だけでなく、細かい単元の正答率を把握 することで、自分の苦手分野に気付くことができる。また、大規模データに基づき典型的な 間違いを分類できれば、 その結果に照らし合わせて、 さらに詳細に自己の学びを振り返るこ とができる。 (公財)日本数学検定協会では、現在「数検スコア診断」の取組を通して、生徒 1 人ひと りの学習到達度を診断する WEB 上の分析診断ツールを提供している。 数学検定・算数検定に は、 個別最適化された学びの学習環境を整える観点からも、 ぜひ客観的なデータに基づき、 自己の学びをより深く把握し、改善に向けた道標を指し示すことができる取組にも期待し たい。願わくば、新しい時代の学校教育において、先生方の普段の授業の営みを支える役割 も担って欲しい。
[1]経済産業省(2019).数理資本主義の時代―数学パワーが世界を変える―. https://www.meti.go.jp/shingikai/ (*)岐阜聖徳学園大学専任講師 economy/risukei_jinzai/pdf/20190326b_report.pdf
- 3 -
�
- ▲TOP

- ページ: 7
- 高校理科における数学活用調査
学習数学研究所 中村 力 要約 前回に引き続き、今回は高等学校の理科(物理、化学、生物、地学)においてどのよう な数学(算数)が使われているかに関する調査を行い、一定の成果が得られたので報告す る。 キーワード:数学、俯瞰チャート、STEM 教育 1.はじめに 前回は、数学が科学や工学の分野で具体的には物理学などの科学、また機械工学、電気 工学、建築・土木工学といった各種工学の分野で、どのような数学的内容・手法が適用さ れているかの調査を実施・報告した(※1) 。 今回は、その継続として高等学校の理科(物理、化学、生物、地学)において、どのよ うな数学(算数)が使われているかの調査を報告する。 2.調査方法 調査方法に関しては、高等学校理科の全国の高等学校で採択率の高い教科書を物理、化 学、生物、地学それぞれ3~4冊ずつ入手し、さらに関連文献やネット情報からの検索な どの情報をもとに調査分析を行った。 すなわち、高校理科、すなわち物理、化学、生物、地学において、小学校の算数、中学 数学、高校数学、大学数学のどのような理論や手法が適用されているかを細かく分析調査 し、前報告(※1)同様に、俯瞰チャートとしてマトリックスに落とし込んだ。 3.調査結果 (1)物理と数学との関連 高校物理の大分類-様々な運動、熱、波、電気と磁気、原子・分子の世界 と 数学の関係をマトリックスにまとめた(図表1:高校物理 俯瞰チャート) 。 全体的にいえるのは、高校物理では各種数学の手法が用いられており、数学と の相関が高く、すなわち数学の依存性が非常に高いことがわかる。 次に物理の各大分類で詳細に見てみよう。
- 4 -
�
- ▲TOP

- ページ: 8
- a.様々な運動 この分野は、いわゆるニュートン力学や古典力学ともいわれる物理の入り口であ る。様々な運動は、常微分方程式である運動方程式を、初期条件を設定することで 解は因果律で定まってしまうが、高校数学でベクトルや微分積分は学ぶものの、物 理の教科書では数学的な厳密性を欠いているものが多い。 これは並行して学ぶ高校数学と同期(学習のタイミング)がとれていないため致 し方ないかもしれない。しかしながら、発展的内容として微分方程式としての運動 方程式の解法を積極的に取り入れている教科書も多くなり、理解が進んだ生徒には 好奇心をそそられる工夫も増してきたように思われる。 b.熱 この分野は、熱力学ともいわれる。特に高度な数学は必要としないが、熱力学の 第1法則として熱収支のイメージ、内部エネルギーの概念の理解を要求される。熱 力学とはアプローチが異なる統計力学(大学物理専攻で学ぶ)では高度な数学も要 求される。熱力学の第2法則に関しては不可逆変化との絡みで抽象的に触れている のみで、これが大学の物理専攻で学ぶエントロピーにつながる記述は見受けられな い。 c.波 時間 t を変数とする常微分方程式であるニュートンの運動方程式とは異なり、 波動 は波動方程式で記述され、波の振幅(強度)を時間 t と場所(空間) x,y, z を変数と する偏微分方程式である。波の解は単純化すると正弦波(時間と空間座標を含む) で記述されるため、この分野は三角関数が多用される。三角関数の合成など物理現 象と絡めて指導してもよいかもしれない。 d.電気と磁気 我々が学ぶ初めての数理的な電気・磁気現象は磁化から受ける電流の力の向き とオームの法則である。前者は、フレミングの左手の法則でベクトルの外積に関連 し、またオームの法則は比例・反比例に関連する。 交流回路では、三角関数とベクトルと複素数と高校で出てくる数学が多用される。 直流では単なるスカラー(位相0)である抵抗が、交流ではインピーダンスと呼ば れ位相をもつ。これは複素数で表すと、非常に見通しがよくなる。 また、電気と磁気の変化はマクスウェルの波動方程式とよばれる偏微分方程式に より統一的に記述される。 e.原子・分子の世界 我々の目に見えない原子・分子の世界は、量子力学で記述されるが、この量子力 学が確立される以前の、古典力学を駆使したボーアの原子モデルが出てくる。さら に、物体が光速の近い速さで運動する場合に適用されるアインシュタインの相対性 理論の入り口を(特殊相対性理論)学ぶ。
- 5 -
�
- ▲TOP

- ページ: 9
- (2)化学と数学との関連 化学も同様に、図表2にてマトリックスにまとめた(図表2:高校化学 俯瞰チ ャート) 。物理に比べると、数学との接点を示す黄色の箇所が少なくなっている。 それに、高校・大学レベルではなく、中学レベルの数学との関連が多い。また、化 学は物理との依存性も高く、例えば量子化学のように物理の量子力学的手法をふん だんに適用している分野もある。 さらに後半の有機化合物や高分子化合物では、化合物の構造が重要な観点で 群論という高度な数学が用いられている。 化学の各大分類で細かく見てみる。 a.物質の状態 比例・反比例など中学レベルの基本的な数学と関連している。 b.物質の変化と平衡 濃度(状態)変化というやや高度な微分という数学に関連してくる。 ただ、これも物理と同様に、高校で学習する数学と学習するタイミング がとれていないために教科書の記述がマッチしていない感じがする。 c.物質の構成粒子 ここは、物理の「原子・分子の世界」とも関連し、量子力学や量子化学 で本格的に学ぶ。偏微分方程式など高度な数学にも関連してくる。 d.無機物質 これは定性的な説明が多く、数学的な記述がほとんど見当たらない。 e.有機化合物と高分子化合物 これらは、化合物の立体構造に関連した構造式の特定にスポットが当てられ、 物質構造の対称性など代数学の群論と関わってくる。 (3)生物と数学との関連 生物の場合、マトリックス図(図表3:高校生物 俯瞰チャート)を見ても、 数学とはほとんど接点がないように見受けられる。ただ、生態と環境のように、 一部高度な数学と関連してくる内容もないわけではない。事実、最近では「理論生 物学」という生物学の先端的な一分野もあるように、生物の種々の側面に関して数 理的な理論やモデルの構築で高度な数学も駆使されているようである。また、生物 は化学との相性もよく、タンパク質や酵素などに関連する生化学という分野もある。 (4)地学と数学との関連 地球は勿論、宇宙まで広範な領域を含む(図表4:高校地学 俯瞰チャート) 。地 球を固体としてみるか、海洋や大気といった流体としてとらえるか、さらに長い時間 軸でとらえる地球史の観点もある。それぞれの領域に対しても数学は駆使されており、
- 6 -
�
- ▲TOP

- ページ: 10
- 数学的手法なくしては、地学は学問として成り立たないといっても過言ではない。 さらに言えることは、地学は、物理学や化学、生物との関連も強く、結局、地学は 数学だけでなく物理、化学、生物とも関連をもつ非常に広汎な学問体系といえるだろ う。 (5)高校理科と数学との概括的な関連 高校理科にどの数学の理論や手法が適用されているかといったマトリックス分析 より、高校理科と数学との関連図(図表5:高校理科と数学の定性的依存関係) を載せた。 定性的な議論になってしまうかもしれないが、高校理科の物理・化学・生物・地学と 数学との相互関連が概略的につかめたかと思う。数学は、物理、化学、生物、地学そ れぞれに関連を持っているが、数学にもっとも関連がある(すなわち、依存している) のが、 物理で、物理>化学>地学>生物 の順であろうと思われる。生物が一番、 数学との関連が少ないように思われるが、最先端の生物の研究では、数理的な理論や モデルの構築で高度な数学を駆使していることについては既にふれた。 また、数学だけでなく、物理、化学、生物、地学間の相互関連性や依存性も重要で ある。物理(的手法)は化学や地学にも大いに関連し、化学と生物との相互依存性も 大きい。地学は、物理、化学、生物すべてから関連性をもつ非常に包括的な学問体制 といえよう。
引用・参考文献 <教科書> (1)物理関連 [1]改訂 新編 物理基礎 啓林館 物理 1 東京書籍 2017 年 第一学習社 2 2018 年 2018 年 2018 年
[2]物理 改訂版 [3]改訂 [4]改訂版 [5]総合物理 (2)化学関連 [6]改訂 新編
高等学校 総合物理 1,2
数研出版 2017 年
啓林館
化学基礎 改訂版 東京書籍 化学 啓林館
東京書籍
2018 年
[7]化学基礎 [8]改訂化学 [9]改訂
啓林館
2017 年
2018 年 2018 年 2017 年
高等学校
[10]化学 改訂版
- 7 -
�
- ▲TOP

- ページ: 11
- (3)生物関連 [11]生物基礎 改訂版 啓林館 2017 年
[12]生物 改訂版 [12]改訂版 生物
啓林館 数研出版 東京書籍
2017 年 2018 年 2018 年
[13]改訂 生物 (4)地学関連
[14]改訂 地学基礎 [15]地学基礎 改訂版
東京書籍 啓林館
2018 年 2017 年
[16]地学 啓林館
2017 年
(5)その他 [17]学習数学研究紀要 創刊号(第1巻) 2018 年 (※1)
数学の科学・工学分野への適用調査
- 8 -
�
- ▲TOP

- ページ: 12
- 除法を使って解く問題に見られる誤答
-算数検定の記述式問題の答案の分析を通して- 学習数学研究所 松本 精一 要約 2018 年 8 月 4 日第 100 回全国算数・数学教育研究(東京)大会幼稚園・小学校部会にお いて、 「実用数学技能検定(算数検定)の答案の考察6」と題した研究発表を行った。本稿 は、このときの研究をもとに答案の調査分析を進めて再構成したものである。 小学校第3学年で初めて除法(整数)を学ぶ。その後、除法の学習は、第4学年及び第5 学年で小数、第5学年及び第6学年で分数と数を拡張しながら進む。 実用数学技能検定 (算数検定) 6級~9級で出題した除法に関する記述式問題の答案を分 析し、 どのような誤答が見られるか、 また階級ごとに誤答の傾向に変化が見られるかを調べ た。その結果、9級では演算決定の誤りが見られ、上の階級に進むにしたがって慣れている 計算に置き換える誤り、除数と被除数を逆にする誤りが見られることが分かった。 キーワード:除法、小数、分数 1 研究のねらい 文部科学省小学校学習指導要領解説算数編に、「A数と計算」の領域のねらいとして、 「整数、小数及び分数の意味や表し方について理解できるようにし、数についての感覚を 豊かにする。また、整数、小数及び分数の計算の意味について理解し、それらの計算の仕 方を考え、計算に習熟し活用することができるようにする。さらに、数の意味や計算の仕 方などの学習を通して、数学的な考え方を育て、算数的活動の楽しさや数理的な処理のよ さに気付いていけるようにすることも大切なねらいである。」とある。 「数と計算」のうち、除法に焦点をあて、整数、小数、分数と数が拡張するのに伴い、ど こに課題が見られるかを、算数検定の記述式問題の答案を資料として調査し分析した。 2 研究の内容(方法) 小学校で学習する除法は、以下の通りである。 ・第3学年:整数の除法(除数と商が1位数)、 簡単な整数の除法(除数が1位数で商が2位数) ・第4学年:整数の除法(除数が1位数や2位数で被除数が2位数や3位数)、 除数が整数の場合の小数の除法
- 9 -
�
- ▲TOP

- ページ: 13
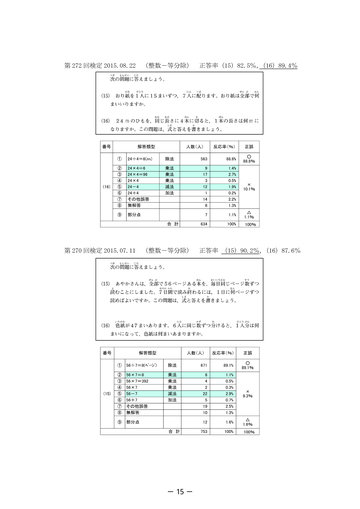
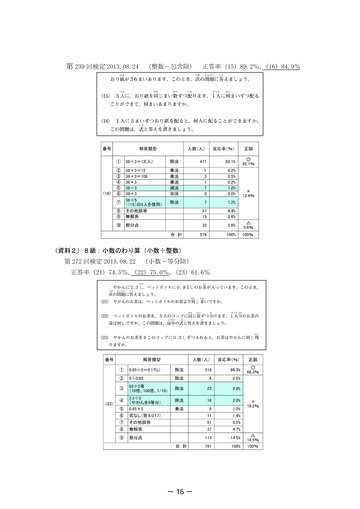
- ・第5学年:除数が小数の場合の除法、除数が整数の場合の分数の除法 ・第6学年:除数が分数の場合の除法 実用数学技能検定(算数検定)には、6級(小学校第6学年程度)から 11 級(小学校第 1学年程度)まで6階級あり、各階級とも2学年分の範囲から出題されている。たとえば、 6級は小学校第6学年及び第5学年が出題範囲である。受検者は自身の学年相当の階級を 選んで受検することが多いため、たとえば6級では受検者のほとんどが小学校6年生であ る。 分析するための問題として各階級とも出題範囲のうちの上位の学年(6級なら第6学年) の記述式問題を選んだ。答案の中から、誤答の答案を抽出し、立式に用いられている演算や 数値等を分類して、どのような傾向があるかを観た。 3 結果 (1)9級:整数のわり算(整数÷整数、乗法九九の逆算) (資料1) 正答率は 80%以上と高く、多くの受検者は除法の学習が定着していると考えられる。 誤答は少なかったが、以下のような答案が見られた。 ・乗法の式を書いて、計算は除法を行っている(解答類型②) 。 除法が乗法の逆算であるため、商を求めるつもりで誤って乗法の式を書いたと考 えられる。 ・乗法の式を立てて、そのまま計算している(解答類型③) 。 除法で商を求めるときに、乗法を用いるために誤って乗法の式を書いてそのまま 乗法の計算をしてしまったと考えられる。 ・年度の早い時期に実施される検定では、減法の誤答が見られる(解答類型⑤) 。 (270 回 7 月、272 回 8 月、239 回 8 月) 分ける、配るなどの操作で減ることを意識して、減法を用いたと考えられる。 ・小問が独立した問題でない場合、前問の数値を用いてしまう(239 回解答類型⑦) 。 いくつかの小問からなる問題を解くことに慣れていないため、他の小問で提示さ れた値を用いてしまったと考えられる。 以上から、除法が用いられる問題に慣れていないために起こる誤答が多いと考えられ る。 (2)8級:小数のわり算(小数÷整数) (資料2) 8級の調査対象の問題はすべて等分除の問題であった。 ・除数と被除数のどちらか一方を 10 倍、100 倍、1/10 等して、整数の除法あるいは 小数同士の除法に変えている(解答類型③) 。 「何十でわるわり算」で、被除数と除数をともに 10 でわっても商が変わらない ことを、誤って用いた可能性がある。
- 10 -
�
- ▲TOP

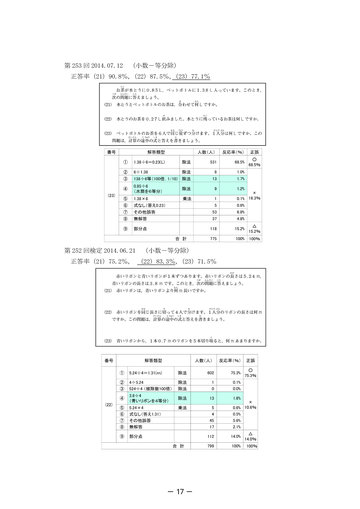
- ページ: 14
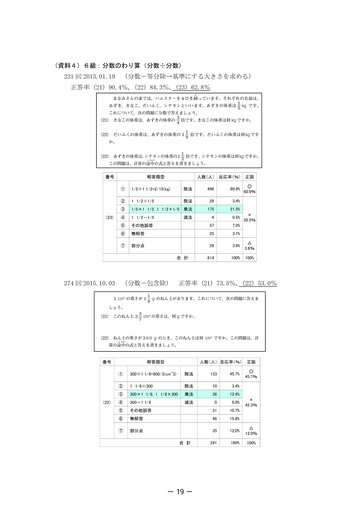
- ・除数は正しいが、被除数に問題文の他の数値を用いている(解答類型④) 。 調査対象の問題はどれも小問が3問ある中での2問めないし3問めの問題であ り、調査対象の問題とは関係のない数値も提示されている。問題を解くために必要 な情報を正しく選べなかったことに起因すると考えられる。 (3)7級:分数のわり算(分数÷整数) (資料3) 7級の調査対象となり得る問題は 239 回の1問(小問番号(24) )だけであった。この 問題が基準にする大きさを求める問題であったためか、他の問題とは異なる傾向が見ら れた。 ・ 「その他誤答」が 30%を占める(解答類型④) 。 「その他誤答」 の中に、 小問番号 (22) で求めた答えを用いた答案が 11.1%、 (23) で求めた答えを用いた答案が 2.8%と多く見られた。 これらの誤答は、 (24) が (22) 、 (23)とは独立した問題であることを読み取れていないことを示している。 ・無解答が 14.3%と多い(解答類型⑤) 。 「無解答」 が多いことから、 問題文の意味を読み取れていないことが考えられる。 リンゴの重さが分数で表されているので、状況を実感できなかった可能性がある。 (4)6級:分数のわり算(分数÷分数) (資料4) 231 回は等分除の問題で、基準にする大きさを求める問題であった。253 回は包含除の 問題で何倍にあたるか(割合)を求める問題であった。他は標準的な包含除の問題であっ た。 ・除法を用いている誤答が多い場合(除数と被除数が逆) (解答類型②) 258 回「油の重さが 3/4kg のとき、この油は何 L ですか。 」 (包含除) 除数、 被除数ともに分数である場合である。 包含除の意味を正しく理解していない と考えられる。 253 回「5/6kg は 7/12kg の何倍の重さですか。 」 (包含除-何倍であるか(割合)を求 める) この問題の誤答の多くが除法を用いた誤りである。何倍かを求めるので除法を用 いることは理解しているが、2数がともに分数であるため、除数(基準量)の決定を 誤ったと考えられる。 ・乗法を用いている誤答が多い場合(解答類型③) 231 回「あずきの体重は、シナモンの体重の 1 1/2 倍です。シナモンの体重は何 kg ですか。 」 (等分除-基準にする大きさを求める) 「1 1/2 倍」というところから、よく考えずに乗法を用いたものと考えられる。 274 回「ねん土の重さが 300gのとき、このねん土は何 cm3 ですか。 」 (包含除) 整数値を用いる場合、除法を用いた(除数と被除数を逆にした)誤答より乗法を用
- 11 -
�
- ▲TOP

- ページ: 15
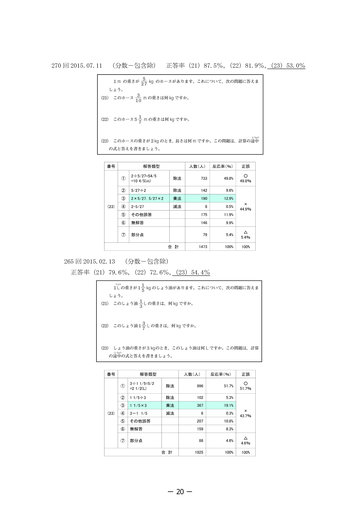
- いた誤答が多くなるようである。270 回「ホースの重さが2kg のとき、長さは何mで すか。 」 、265 回「しょうゆの重さが 3kg のとき、このしょう油は何 L ですか。 」も同 様である。 258 回「油の重さが 3/4kg のとき、この油は何 L ですか。 」 (包含除) 除数、 被除数ともに分数である場合は、 除法を用いた誤答がもっとも多い (19.3%) が、乗法を用いた誤答も 11.5%と多く現れる。 また、調査対象の問題について、253 回の問題以外はすべて直前の小問が乗法の問題 である。それに影響されて乗法を用いた可能性も考えられる。 4 まとめ (1)整数の除法 全体的に正答率が高く、誤答は少ない。 9級(小学校第3学年程度)では、乗法及び減法を用いた誤答が見られる。乗法で書か れた答案の中には式は乗法で、 計算は除法を行い答えは正解というものがある。 減法を用 いる誤答は 11 月以降には減る傾向にある。上記は新出の演算に慣れていないことに起因 する誤答のようである。ただし、分析した問題では、小問同士が完全に独立している問題 が多いため、除法での誤答が現れにくかったことも考えられる。239 回では、前問に影響 された除法を用いた誤答も見受けられた。 (2)小数の除法 8級(小学校第4学年程度)で出題した除数が整数の場合の除法では、被除数を 10 倍 したり 100 倍したりしている誤答、その問題とは関係がない値を使っている誤答等が見 られる。 これ以前に学習する整数の除法とは異なり、 数の大小関係だけでは除数と被除数 が決まらないことに対処できていない印象である。 7級(小学校第5学年程度)では、その問題の前の小問の答えの値を用いている誤答が 見られる。問題がやや複雑になり、意味を正確に把握していないために、必要な値を選べ ないと考えられる。 (3)分数の除法 6級(小学校第6学年程度)では、除数と被除数が逆になっている誤答、乗法を用いた 誤答が見られる。 小数の除法と同様に、 問題を正確に読み解いて除数と被除数を決定する ことに課題が見られる。
- 12 -
�
- ▲TOP
- ページ: 16
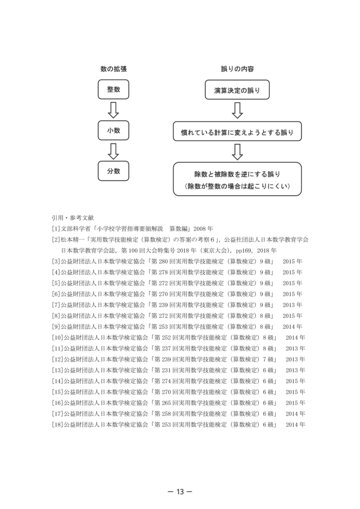
- 数の拡張 整数
誤りの内容 演算決定の誤り
小数
慣れている計算に変えようとする誤り
分数
除数と被除数を逆にする誤り (除数が整数の場合は起こりにくい)
引用・参考文献 [1]文部科学省「小学校学習指導要領解説 算数編」2008 年
[2]松本精一「実用数学技能検定(算数検定)の答案の考察6」 ,公益社団法人日本数学教育学会 日本数学教育学会誌,第 100 回大会特集号 2018 年(東京大会) ,pp169,2018 年 [3]公益財団法人日本数学検定協会「第 280 回実用数学技能検定(算数検定)9 級」 [4]公益財団法人日本数学検定協会「第 278 回実用数学技能検定(算数検定)9 級」 [5]公益財団法人日本数学検定協会「第 272 回実用数学技能検定(算数検定)9 級」 [6]公益財団法人日本数学検定協会「第 270 回実用数学技能検定(算数検定)9 級」 [7]公益財団法人日本数学検定協会「第 239 回実用数学技能検定(算数検定)9 級」 [8]公益財団法人日本数学検定協会「第 272 回実用数学技能検定(算数検定)8 級」 [9]公益財団法人日本数学検定協会「第 253 回実用数学技能検定(算数検定)8 級」 [10]公益財団法人日本数学検定協会「第 252 回実用数学技能検定(算数検定)8 級」 [11]公益財団法人日本数学検定協会「第 237 回実用数学技能検定(算数検定)8 級」 [12]公益財団法人日本数学検定協会「第 239 回実用数学技能検定(算数検定)7 級」 [13]公益財団法人日本数学検定協会「第 231 回実用数学技能検定(算数検定)6 級」 [14]公益財団法人日本数学検定協会「第 274 回実用数学技能検定(算数検定)6 級」 [15]公益財団法人日本数学検定協会「第 270 回実用数学技能検定(算数検定)6 級」 [16]公益財団法人日本数学検定協会「第 265 回実用数学技能検定(算数検定)6 級」 [17]公益財団法人日本数学検定協会「第 258 回実用数学技能検定(算数検定)6 級」 [18]公益財団法人日本数学検定協会「第 253 回実用数学技能検定(算数検定)6 級」 2015 年 2015 年 2015 年 2015 年 2013 年 2015 年 2014 年 2014 年 2013 年 2013 年 2013 年 2015 年 2015 年 2015 年 2014 年 2014 年
- 13 -
�
- ▲TOP

- ページ: 17
- (資料1)9級:整数のわり算(整数÷整数、乗法九九の逆算) 第 280 回検定 2015.12.05 (整数-等分除) 正答率 (15)93.4%, (16)87.0%
第 278 回検定 2015.11.14 (整数-等分除) 正答率 (15)93.5%, (16)80.8%
- 14 -
�
- ▲TOP
- ページ: 18
- 第 272 回検定 2015.08.22 (整数-等分除) 正答率(15)82.5%, (16)89.4%
第 270 回検定 2015.07.11 (整数-等分除) 正答率 (15)90.2%, (16)87.6%
- 15 -
�
- ▲TOP
- ページ: 19
- 第 239 回検定 2013.08.24 (整数-包含除) 正答率(15)89.2%, (16)84.9%
(資料2)8級:小数のわり算(小数÷整数) 第 272 回検定 2015.08.22 (小数-等分除) 正答率(21)74.5%, (22)75.0%, (23)61.6%
- 16 -
�
- ▲TOP
- ページ: 20
- 第 253 回 2014.07.12 (小数-等分除) 正答率(21)90.8%, (22)87.5%, (23)77.1%
第 252 回検定 2014.06.21 (小数-等分除) 正答率(21)75.2%, (22)83.3%, (23)71.5%
- 17 -
�
- ▲TOP

- ページ: 21
- 第 237 回検定 2013.07.13 (小数-等分除) 正答率(24)93.1%, (25)63.1%, (26)60.9%
(資料3)7級:分数のわり算(分数÷整数) 239 回 2013.08.24 (分数-等分除→基準にする大きさを求める) 正答率(22)73.8%, (23)56.0%, (24)48.0%
- 18 -
�
- ▲TOP
- ページ: 22
- (資料4)6級:分数のわり算(分数÷分数) 231 回 2013.01.19 (分数-等分除→基準にする大きさを求める) 正答率(21)90.4%, (22)84.3%, (23)62.8%
274 回 2015.10.03 (分数-包含除) 正答率(21)73.5%, (22)53.0%
- 19 -
�
- ▲TOP
- ページ: 23
- 270 回 2015.07.11 (分数-包含除) 正答率(21)87.5%, (22)81.9%, (23)53.0%
265 回 2015.02.13 (分数-包含除) 正答率(21)79.6%, (22)72.6%, (23)54.4%
- 20 -
�
- ▲TOP

- ページ: 24
- 258 回 2014.10.17 (分数-包含除) 正答率(21)81.6%, (22)82.8%, (23)49.7%
253 回 2014.07.12 (分数-包含除→何倍になるか(割合)を求める) 正答率 (21)66.1%, (22)35.4%, (23)44.2%
- 21 -
�
- ▲TOP

- ページ: 25
- 数検答案から見た数学教育の問題点
-公式に頼る数学教育から数学を楽しむ数学検定へ- 日本数学検定協会 渡辺信 要約 数学検定の 3 級 1 次には方程式を解く問題がある。この中で 2 次方程式の解法について 不思議な結果が出ている。易しいと思われる問題のほうの正答率が低い。この結果は最近 の特徴ではなく、前からおかしいと思われていたことである。今回、授業参観の機会が与 えられ、公式に頼る数学教育を見ることができた。会の公式を使えばどのような 2 次方程 式も解けることを前提とし、公式の活用の訓練の教育が行われている。数学を楽しむ学習 の方向へと授業改善が望まれる。 キーワード:公式活用の数学教育 2次方程式と解の公式 正答率 数学検定 1.数検解答正解率からの不思議 数学検定の 3 級 1 次の問題の中に 2 次方程式を解く問題がある。この問題の正答率に不 思議な数値を見つけた。 中学校の段階では 2 次方程式を因数分解する方法は範囲外であり、 完全平方を作ることも難しいのかもしれない。 そうなると 2 次方程式を解くことは、 解の公 式が解法の手段になる。しかし、もっとも根本的な「2 乗したら a になる数」という数学の 意味を失っているのではないかと思われる。 問題 次の方程式を解きなさい。 (正答率) 3x2-72=0 x2-3x-5=0 53.5% 64.5
この 2 つの方程式は並んで出題されている。出題者は前の 2 次方程式のほうが易しいと 思い並べているに違いない。 しかし、 正答率からみると後半の方程式のほうがよく解けてい る。この傾向はいつも同じ結果になる。 一般には数学教育では易しいことから難しいことへという順番であり、基本から応用と 順を追って学ぶ。初めは係数は数を考えている。 x2=4 → x=±2(答えに±が付くことが強調されている) (x-1)2=3 → x-1=±√3 → x=1±√3(完全平方を作るのは難しい) x2-2x―3=0 → (x-1)2=4 → x-1=±2 → x=3、-1
- 22 -
�
- ▲TOP
- ページ: 26
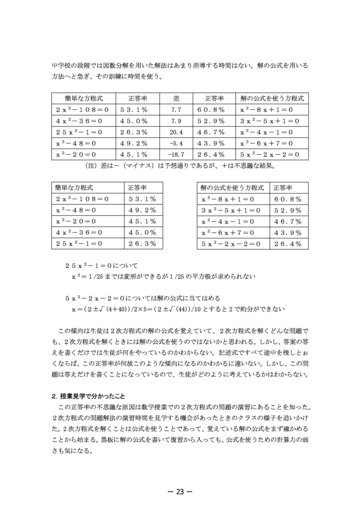
- 中学校の段階では因数分解を用いた解法はあまり指導する時間はない。解の公式を用いる 方法へと急ぎ、その訓練に時間を使う。 簡単な方程式 2x2-108=0 4x2-36=0 25x2-1=0 x2-48=0 x2-20=0 正答率 53.1% 45.0% 26.3% 49.2% 45.1% 差 7.7 7.9 20.4 -5.4 -18.7 正答率 60.8% 52.9% 46.7% 43.9% 26.4% 解の公式を使う方程式 x2-8x+1=0 3x2-5x+1=0 x2-4x-1=0 x2-6x+7=0 5x2-2x-2=0
(注)差は-(マイナス)は予想通りであるが、+は不思議な結果。 簡単な方程式 2x2-108=0 x -48=0 x2-20=0 4x2-36=0 25x -1=0
2 2
正答率 53.1% 49.2% 45.1% 45.0% 26.3%
解の公式を使う方程式 x2-8x+1=0 3x -5x+1=0 x2-4x-1=0 x2-6x+7=0 5x -2x-2=0
2 2
正答率 60.8% 52.9% 46.7% 43.9% 26.4%
25x2-1=0について x2=1/25 までは変形ができるが1/25 の平方根が求められない 5x2-2x-2=0については解の公式に当てはめる x=(2±√(4+40))/2×5=(2±√(44))/10 とすると 2 で約分ができない この傾向は生徒は2次方程式の解の公式を覚えていて、2次方程式を解くどんな問題で も、2次方程式を解くときには解の公式を使うのではないかと思われる。しかし、答案の答 えを書くだけでは生徒が何をやっているのかわからない。記述式ですべて途中を残しとぉ くならば、この正答率が何故このような傾向になるのかわかるに違いない。しかし、この問 題は答えだけを書くことになっているので、生徒がどのように考えているかはわからない。 2.授業見学で分かったこと この正答率の不思議な原因は数学授業での2次方程式の問題の演習にあることを知った。 2次方程式の問題解法の演習時間を見学する機会があったときのクラスの様子を追いかけ た。2 次方程式を解くことは公式を使うことであって、覚えている解の公式をまず確かめる ことから始まる。 黒板に解の公式を書いて復習から入っても、 公式を使うための計算力の弱 さも気になる。
- 23 -
�
- ▲TOP

- ページ: 27
- 先生 x2-20=0を解きなさい。 生徒 x=・・・分母は2だけど、bがない。 先生 ないところはb=0です。 生徒 分子は-0±√(02-4×1×20) この計算ができない。 先生 02は0だから計算は簡単でしょ。 生徒 √(4×1×20)=√80 先生 それで 生徒 答え x=√80 これでは、 いつまでたっても答えは出てこない。 同じ生徒に問題を変えてといてもらった。 先生 この問題と解いてください x2-8x+1=0 生徒 こちらのほうが易しい x=-8±√(64-4)を2で割る。 先生 bの符号はどうするの 生徒 ・・・ おそらくこの後の計算変形ができない。ここで分かったことは先生は徹底的に2次方程 式の解の公式を覚えさせている。 そして公式を使えば、 どんな2次方程式でも解くことがで きると教えている。 今回見学をさせてもらった学校が特殊なのではなく、 公式を使えば2次 方程式は解けるということを徹底して学んでいる結果が、数学検定の正答率に現れている。 そして、もっとも基本的な考え方として x2=a のとき、x=±√a は忘れている。こ の式を見ると a の符号について問題にする生徒がいるのは先生が授業中に何を重要として 教えているかが推測できる。 ルートの中はプラスということを徹底しているので、 生徒は符 号がなくなってしまうらしい。 公式を覚えていても計算ができない。 ルートの計算も難しい ので解の公式を知っていても、途中にルートの計算、約分などがあり、最後まで2次方程式 を解くことは難しい。 3.公式に頼らない数学教育を (1)公式不要 電車の中吊り広告 「公式に頼らない図形脳」と いうある予備校の広告があった。 その広告の対象は 幼稚園児に出題する問題であった。 図の中に立方体 (四角い積み木)がいくつあるかを数える問題であ る。この問題に使える公式ないし、幼稚園児は、ひ とつずつ数える。見えない積み木を数えるという、 「公式に頼らない」という言葉に興味を持った。 この 問題では、 考え方(数学的戦略)を問うこととして次
- 24 -
�
- ▲TOP

- ページ: 28
- のような説明があった。 隠れている部分を見るために、 手前の 3 個の積み木を前に引き出す ことを戦略にし、 図形の個数を数え上げるためには公式などに頼らず、 数学を考えることが 大切であるということを伝えているのではないかと思われた。図形に対する問題に対して 公式というのには少し違和感を持ったが、 数学は公式に頼るのではなく、 自ら考えることが 大切ということを語るとともに、現在の数学教育に対する警鐘として広告を見た。 (2)授業参観では 2 次方程式の解法は公式の利用の訓練 ある学校の数学の授業では 2 次方程式の解を求める授業であった。このとき黒板にまず 2 次方程式の解の公式が書いてあり、いつでも使えるようになっていた。そして授業の開始 と同時に、 2次方程式の解の公式を唱えながら記憶した公式を再確認していた。 この授業で は公式の使い方の訓練だけで、生徒にとって数学の問題を解くことはおもしろいとは思わ なかったであろう。 あまりに公式に頼り過ぎていて、 公式に数値を代入するだけの授業では 面白さが伝わってこない。 その時に約分があったり、 ルートの中の整理をしなくてはならな かったり、難しい問題に躓いていた。授業風景は、x2+2x-3=0を生徒が解く過程を 示しながら黒板に答えを書いていた。 因数分解を用いるのではなく解の公式を使って、解が求まればよいという感じで数学の 授業は公式を用いて解を求めるという訓練が行われている。 x=(-2±√22-4×(-3))/2 =(-2±√16)/2 =(-2±4)/2 =2/2、-6/2 =1、-3 このくらいで黒板に書くことが終われば良い方で、まだまだ指導することが多い感じが した。 まさに「公式に頼る」数学授業でしょう。 この授業に対しては「公式に頼らない」という 言葉はすばらしい言葉なのではないかと思う。 x2+ax+b=0の解をα、βとすると、 α2+aα+b=0・・・(1) β2+aβ+b=0・・・(2) (1)-(2) α2-β2+a(α-β)=0 (α-β)( α+β+a)=0 これから何が分かる? (3)鶴亀算は何故公式を使わない? 鶴亀算の問題では生徒がいくつかの方法を示した。問題は有名な鶴亀算であった。 公式を見ながらていねいに数値を代入 ルートの中の計算 √16=4は難しい ±の扱い方/約分
- 25 -
�
- ▲TOP

- ページ: 29
- 問題(鶴亀算) 鶴と亀、 合わせて12匹、足は全部で30本です。このとき鶴と亀はそれぞれ何匹です か。 解法1(和算による) 12匹すべて亀であったとすると足は48本。 48-30=18 18本足りないのは鶴の足が2本であるから 18÷2=9 答え 亀3匹、鶴9匹 解法2(図解による解法) はじめに12個の○を書く(亀・鶴を○で示す) ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○
すべては2本の足を持つので、点を2個つける、(点は2×12=24個) ・・ ・・ ・・ ・・ ・・ ・・ ・・ ・・ ○ ○ ○ ○ ○ ○ ○ ○ ○ ・・ ・・ ・・ ・・ ○ ○ ○
残っている点が30-24=6(6点を付ける) ・・ ・・ ・・ ・・ ・・ ・・ ・・ ・・ ○ ○ ○ ○ ○ ○ ○ ○ ○ ・・ ・・ ・・ 4本の足を持つ亀は3匹、残りは鶴で9匹。 解法3(代数を用いる) 鶴を x 匹、亀を y 匹とする x+y=12 2x+4y=30 この連立方程式を解く x=9、y=3 解法4(公式を作る)・・・この公式を見たことはない、何故? 鶴と亀合わせてa匹、足の本数をb本とする 公式(a、bの範囲も明示 x=(4a-b)/2・・・鶴 y=(b-2a)/2・・・亀 ・・ ・・ ・・ ・・ ○ ○ ○
- 26 -
�
- ▲TOP

- ページ: 30
- 公式を作ったことはないが、鶴亀算を何回も訓練するなら公式は便利かもしれない。何 故、公式を今まで作らなかったのか、あまり考えたことはない。我々の数学教育は公式ば かりであるが、なぜか鶴亀算には公式を使うという考え方はなかった。 4.数学教育の改革を 現在の試験では答えを選択肢の中から選ばせる方法が多い。選択方式で生徒がどのよう に考えたかということはわからない。センター試験がマークシート利用であることが問題 にもなっている。 このような方式では生徒がどのように考えたか、 途中経過はわからない。 数学の問題を解くことの訓練は、問題と同時にその解法・戦略をも与えられている。数学は 論理的思考方法を訓練するのであれば、どのような考え方をしたかを評価する必要がある。 高大接続問題が数学教育に記述式を導入することを提示してから、いろいろな方面から記 述式の重要性が示されている。数学検定協会の実施する数検での答えは記述式で行われて いる。参加する生徒はきちんと答案を書くことができるが、書くことは苦手である。これは 日常の数学教育が問題を見たら即座に答えるということを重視しているのではなかろうか。 最近、数学の重要性が指摘される。AI における数学活用、データ・サイエンスに必要な 数学、 コンピュータ普及によるテクノロー使用など、 いたるところに数学が使われるように なっている。しかし、ここで数学として指し示すことは何かを考えたい。数学の重要性とし ての数学は、 高校までに学ぶ数学知識を指すのではない。 非常に高度な数学を指すのであっ て数学の専門家の必要性を語るのかもしれない。しかし、数学の考え方ではなく、使われて いる数学の公式を必要とするのではなかろうか。 公式を覚えておけば、 どのような 2 次方程 式でも解けると同じように、 公式だけが必要な数学になるのではなかろうか。 数学の公式を 覚えて使うことは数学ではない。現在必要な数学とは、数学的思考方法であるが、この訓練 の道は遠い。 5.数学検定の在り方 問題の答えだけを求めても、 その検定受検者の考え方はわからない。 選択式では偶然に正 解を選ぶこともありうる。選択肢が 4 つあるとき正答率が 0.25(1/4)となることは、全 員が全く分からないことを表すと考えられるので、正答率だけを見ていても数学能力が身 についているかはわからない。きちんと受検者の数学的思考力を認定するためには記述式 が重要である。 実際に受検者の考えた過程を見ることによって、 数学能力を保証することが できる。この意味において答えを書くことの記述式を数学検定が重んじることは重要であ る。 今回の調査結果は正答率から不自然さを見つけた。易しいほうがは難しい問題よりも正 答率が低いという不自然さがどこから生じるのかを追いかけた結果、数学が公式の訓練に なっていることが明らかになった。 多くの答案を見ることによって、 数学教育の在り方を検 証できることは、検定を行うことの意味がある。検定は個人の能力保障だけではなく、多く
- 27 -
�
- ▲TOP

- ページ: 31
- の人々の結果を見ることによって、数学教育において何が問題あの課をも指摘することが できる。公式を覚えて、その公式を使う訓練では、数学が楽しくはならない。 数学検定の問題の在り方として、 技能的な能力の保証も重要な資格認定であるが、 問題を 解く楽しみを体験できることが重要である。 検定問題を解き、 その結果から能力認定を得る と同時に、数学の楽しさを伝えることが可能になる問題を作成することが重要であること を今回の 2 次方程式の解法の問題が語っていた。
引用・参考文献 [1] 公式に頼らない図形脳,日能研電車広告,2019 [2]Ken Johnson & Ted Herr,Problem Solving Strategies, Key Curriculum Press, 2001
- 28 -
�
- ▲TOP

- ページ: 33
- 2次行列の累乗について
学習数学研究所 特別顧問 一松 信(*) 0.はじめに
a b n 2次行列 A= の累乗 A の計算は,数学検定の1級(ときに準1級)によく出題さ c d
れている。 それは標準的な手法によって対角化を (それが不可能ならばジョルダンの標準形 に)して容易に計算できる。その意味で典型的な課題であり,何次でも同様である。 しかし2次に限れば, 以下のようにスペクトル分解の応用による 「ずるい」 計算法がある。 このような方法は, 線形代数学の 「王道」 とはいえない。 将来高校数学に行列が復活しても, 標準課程に取り入れるべきではないと思う。 しかし出題者の立場から見ると, こういった解法もあることを考慮に入れて, 慎重に出題 することが望ましい。 そのような注意を喚起する意味で, 敢えて本稿を執筆した次第である。 以下行列の成分は任意の体の要素でもよいが,実数として述べる。また一般の n 次正方 行列についても同様だが, 解説を2次行列に限定する。 固有値を含む線形代数学の基礎知識 は既知とする。 1.行列の固有値に関して(復習) 2次の正方行列 A は R 2 から R 2 への線形写像の表現である。それによって自分自身の (0でない)定数倍に写される(0でない)ベクトル v:Av =λv が固有ベクトルであり, 定数λは固有値とよばれる。 これに対して uA=λu(u≠0)を満たす行ベクトル(横ベクトル)u を行固有ベクトル とよぶ。それは A の転置行列 A T の固有ベクトルを転置したものである。 固有値λは固有方程式 det(A-λI )=0 の解として計算できる(det は行列式,I は
a b 単位行列) 。今の場合 A= に対して,固有方程式は c d
2 λ - (a+d ) λ+ (ad-bc) =0
⑴
と表される。 以下しばらく⑴が相異なる2個の解λ1, λ2 をもつ (判別式≠0) と仮定する。 λi(i =1,2)に対する(列)固有ベクトルと行固有ベクトル(の1つ)をそれぞれ v i, u i とおく。v 1 ,v 2 ; u 1 , u 2 はそれぞれ一次独立で,それぞれが R 2 の基底をなす。 補助定理1 u 1 ・v 2 =0, u 2 ・v 1 =0,s i=u i・v i≠0 証明 u 1 ・A・ v 2 =λ1 u 1 ・v 2 =λ2 u 1 ・v 2 であり, λ1 ≠ λ2 から u 1 ・v 2 =0;u 2 ・v 1 =0も同 様。他方 u 1 は u 2 と一次独立なので, s 2 =u 2 ・v 2 ≠0; s 1 =u 1 ・v 1 ≠0も同様である。▯ 注意 A が対称行列なら u i は v i の転置行列としてよいが,そうでない場合には区別を要
(*)SIN HITOTUMATU,京都大学名誉教授,公益財団法人 日本数学検定協会名誉会長
- 29 -
�
- ▲TOP

- ページ: 34
- する。なお上記の積は u i を1行2列, v i を2行1列の行列とみなしたときの行列の積であ る。 2.スペクトル分解 前節の記号をそのまま続けて使う。 補助定理2 Pi=
1 v i・u i (2行2列の行列) si
⑵
とおくと,行列 P1 ,P2 は次の性質をもつ: Pi2=Pi ,P1 ・ P2 =P2 ・P1 =O (零行列) P1 +P2 =I,λ1 P1 +λ 2 P2 =A 証明 ⑶は単なる計算でできる。行列の積に結合法則を適用する。 Pi2=
s 1 v i・u i・v i・u i= i2 v i・u i=Pi 2 si si
⑶ ⑷
(i =1,2)
P1 ・ P2 =
1 v 1 ・u 1 ・v 2 ・u 2 =O,P2 ・P1 も同様。 s1 s2
⑷は次のように考える。任意の(縦)ベクトル x は,一意的にα1v 1 +α2v 2 と表される。 これに⑷の左辺の行列を,線形変換として適用する。i ,j=1,2として Pi v j =
s 1 v i・u i・ v j = i v i・δi j si si
(j = i なら v i ,j≠i なら0)
だから,次の等式が成立する。 (P1 +P2 )x =α1v 1 +α2v 2 = x =I x (λ1 P1 +λ2 P2 )x =λ1 α1v 1 +λ2 α2v 2 =Aα1v 1 +Aα2v 2 =Ax これらがすべてのベクトル x に対して成立する。これは両辺の写像を表す行列どうしが 相等しい(式⑷)ことを意味する。▯ 定義 上述の性質⑶,⑷を満たす2次行列 P1 ,P2 をもとの行列 A のスペクトル分解と いう。それは式⑷を P1 ,P2 の連立一次方程式とみなせば一意的である。▯ 実用上には⑷を解いて,次のように直接に計算するほうが早い。 P1 =
1 1 (A-λ2 I ) ,P2 = (λ1 I-A) λ λ 1-λ 2 1-λ 2
⑸
3.Aの累乗の式 定理3 スペクトル分解 P1 ,P2 が既知とする。λ1 ≠ λ2 のとき,A の累乗は次の式で与 えられる。 An=λ1nP1+λ2nP2 ⑹
- 30 -
�
- ▲TOP

- ページ: 35
- 系 もしλ1 ≠0,λ2≠0ならば,A の逆行列 A-1 は⑹で n=-1とおいた式 で与えられる。
1 1 P1+ P2 λ λ 1 2
証明 n=0,1のときは補助定理2による(A0=I とみなす) 。次に n>0のとき正しい とすれば An+1=An・A=(λ1nP1+λ2nP2) (λ1P1+λ2P2) =λ1n+1P1+λ2n+1P2+ (λ1nλ2・P1・P2+λ1λ2nP2・P1) n+1の場合になる。すなわち n に関する数学的帰納法で正しい。 系は同様に,n=-1とした式に A=λ1 P1 +λ2 P2 を掛ければ P1 +P2 =I になるので,そ れが逆行列である。▯ 以上によって A の固有値λ1 ,λ2 (但しλ1 ≠λ2 )さえ計算できれば,A の累乗もさらに 逆行列(λ1λ2 ≠0のとき)も,対角化行列などを計算せずに,直接に計算できる。
4 1 例1 A= 8 6
2 固有方程式はλ -1 0 λ+1 6=0であり,固有値はλ1 =8,
⑺
だ が , P1・P2 =P2 ・P1=O(零行列)で⑺の末尾の( )内は O に等しく,⑺は⑹の
λ2 =2;式⑸から P1 =
2 1 1 1 4 -1 , P2 =6-8 2 8 4 6
n 8 6
であり,累乗は次のようになる。 An=
3n+1 n+2 n n n 2 1 2 4 -1 1 2 +2 8 -2 + = n 1 n+3 3n+2 n+1 8 4 6 -8 2 68 -2 2 +2
必要ならば A を対角化して検算してみるとよい。 4.固有値が重解の場合 固有方程式⑴が重複解λをもつ場合には, 上述の方法は適用できないが, 伝統的な標準手 法で累乗 An が計算できる。 もしも重複固有値λに属する固有ベクトル空間が2次元ならば,A は(λ,λ)を対角線 成分とする対角線行列に変換できる。しかしそれは初めから A=λI の場合であって,計算 は容易である。 それ以外の場合には A は対角化できない。しかし(いろいろな方法で)適当な可逆な変 換行列 M により
λ 1 B=M -1AM= =λI + J , J = 0 λ 0 1 0 0
とジョルダンの標準形に変換できる。J 2 = O であり
n An=MB nM -1;B n=(λI + J ) =λnI + n λn-1J
の形で A の累乗が計算できる。具体的には次の通りになる。
- 31 -
�
- ▲TOP

- ページ: 36
- An=λnI + n λn-1(MJM -1)
p q p M= とおくと,MJM -1= ps-qr r s 2 -1 例2 A= 1 0 -r p -p r
⑻
結局変換行列 M を求めることができれば,式⑻により An が計算できる。
2 2 固有方程式はλ 固有値は1 (重解) -2 λ+1 = (λ-1) =0で,
1 だが,固有ベクトル空間は1次元である。その一例は v = 。 1
1 1 1 (A-λI ) w =v である一般固有ベクトル w の一例は w = 。M=[v w ]= , 1 0 0 1 1 0 1 1 n -1 n M-1= であり, となる。B =I + nJ= により,B=M AM= 0 1 1 -1 0 1 n+1 -n An=MB nM -1= を得る。 1 -n n
⑼
ジョルダンの標準形に変換する行列 M は他にもあるが,An の結果は同一である。結果の 式⑼がわかれば,それが正しいことは,n に関する数学的帰納法で確かめられる。 5.むすび 以上の議論はある程度一般の正方行列に拡張できるが、特に2次の場合の簡便法に重点 を置いた。初めに述べた通り,こういった「安直な便法」が広まるのは必ずしも望ましいと は思われない。しかし出題者側は十分心得ていてほしい知識として紹介した次第である。
- 32 -
�
- ▲TOP

- ページ: 37
- 直線上の点 E で AEn+BEnを最小とする点 E の位置変化
学習数学研究所 渡辺信 有名な対称点を取る問題を変形して新しい問題に挑戦することを試みた。問題から新し い問題を作り、 はじめの問題を発展していくことは、 自ら作り出した数学を考えるためには 非常に有意義である。そして、作り出した問題の解は、問題作成中に見えてくる。
問題 直線の上側に点A,Bがあって、直線上に点 E を取る。 AE+BE の長さが最短のときの点Pの位置をもとめよ。
この問題の解答は、点 B の直線に対する対称点 B’を取り、 AB’と直線の交点を E とすればよい。(図1) 図 1 点を一つ加えて、点 A,B,C があって、AE+BE+CE の最小問 題にしたが、これは解けていない問題らしい。数学ソフト を用いてみたがわからない。簡単な拡張問題が解けないの は不思議である。そこで、点の位置を変えてみることにし た。 点 A,B は固定されていて動かすことは考えない。点 B は 固定し、点 A を上下に動かしたら E 点 E の位置は直線上ど のように動くかは、点 B’が固定されていることより、直線 上を左(点 B のほう)に動く。 点 B の対称点を取ることで問題は解決したが、楕円の規則 を学んだあとでは、この問題を楕円との関係で缶が得ること もできる。点 E を見つける方法として楕円と直線との接点が 話題になった。点 E が乗っている直線を円に変えることに よって楕円がその解決方法に強力な道具になることも分かっ た。(図2) 図2 座標を考え、式で表して微分を行えばよい。必ず最小になる点 E が存在することは明ら かであり、極点を求めればよいことはわかる。数学における重要な問題の一つは最小・最 大を求める問題であり、計算では微分が使われる。いろいろな条件を付けたときの直線上 の点位置を求めてみたい、どのように変化するか見たいと思う。計算の訓練をするのでは
- 33 -
�
- ▲TOP

- ページ: 38
- なく、点 E の位置を知りたい。
点 A(0,4) 点 B(7,2)
次に拡張を考えたのは、AEn+BEnの自然数nを変えてみた。 点 A(0,4)、点 B(7,2)、点 E(x,0)とする。 (図 3) n=1 L =AE+BE =√(x2+42)+√((x-7)2+22) Solve(dL/dx=0,x) x=14/3=4.666… この座標は対称な点から求めた場所と同じ n=2 L2=AE2+BE2 =√(x2+42)2+√((x-7)2+22)2 Solve(dL2/dx=0,x) x=7/2
3 3
E(x,0) 図3
中点
n=3 L =AE +BE3 =√(x2+42)3+√((x-7)2+22)3 Solve(dL3/dx=0,x) x=3.19499… n=4 L4=AE4+BE4 =√(x2+42)4+√((x-7)2+22)4 Solve(dL4/dx=0,x) x=3.05272…
nの値 1 2 3 4 点 E の位置 14/3=4,666… 7/2=3.5 3.19499… 3.05272… 参考 対称点 中点 長いほうに寄って来る
一般にnを大きくしていくと、Ln=AEn+BEnの値はnの増加に対して、点 E は高い位 置の点Aの方向にx軸上近づいていくことがわかる。計算機の関係で点 A,B を一般の位置 にできず、特定の点としたが、これは一般の位置にしても変化はない。証明をしない数学 は認めないと考えられるが、自らが考え出した数学の答えが見つかることは楽しい。この 考え方を証明としてまとめてみることが今回は行わなかった。 また、途中の微分計算はnが奇数のときは非常にめんどくさい。答えを知りたいときに は計算の途中は省くことができる。微分の計算は計算ソフトを利用した。
- 34 -
�
- ▲TOP

- ページ: 39
- 次の問題は、点 E が乗っている直線をほかの曲線に変える問題である。 直線を円にした場合
直線を円にする
この場合は直線の対象点を考えたことを、 演習の曲線による対称点と考えたいが、 曲線に対 する対称点はわからない。 そこで対称点を用いない方法を考える必要があり、 楕円を用いる ことが有効である。 楕円は AE+BE が一定な点の集合ということと、 はじめの問題との関連が 指揮の上からわかる。 楕円を用いて、円との接点を求める。 点 A、B が外部にある場合も楕円を用いて考えら れる。
今後、 この問題をいろいろと変形したときに、 どのような新しいことが発見できるかを考 えたい。問題の条件を変えるということによって、いろいろな問題が作られるであろう。問 題発見とその答えを見つける数学は楽しい。
- 35 -
�
- ▲TOP

- ページ: 40
- 大学に向けた記述式の提案
学習数学研究所 松本 精一 中央教育審議会は高大接続改革において『記述式』を提案しています 入学試験・新入生学力調査などに『数検』を活用しませんか 選択式・穴埋め式の数学試験では、数学の本当の力は測れません。 「数学検定」の問題は 発足当初から「記述式」の答を求めてきました。そして、生徒が考える楽しさを味わえる問 題を作成しています。 数学は考えることが重要ですので、 考えを自由にまとめる作業ができ る「記述式」を行ってきました。 最近、 高大接続検討委員会で問題の解答方法を 「記述式」 にすることが検討されています。 そして、 「記述式」 での採点の困難・公正さなど、 数学の本質から離れたことが話題になり、 「記述式」導入に躊躇しています。しかし、生徒の数学の力を知るためには「記述式」が絶 対に必要です。入学試験で数学の問題を「記述式」にすることは、いろいろな問題点があり 難しいでしょう。しかし、数検は記述式にこだわります。 数学検定協会の問題とその問題に対する「記述式」の生徒の答案を見てください。みなす ばらしい答案を作ります。問題にはヒントがありません。誘導式でもないので、その場でい ろいろと試行錯誤をした後で、きちんと書かれた答案です。
日本数学検定協会が「記述式」を重んじる理由 当協会の行う「実用数学技能検定」 (数学検定・算数検定)は、検定によって人をふるい 分けるというものではありません。当協会は、いかに多くの「数学が好きな児童・生徒・学 生・社会人を育てる」かが大切であると考えています。数学の問題を解くことを通して、数 学を楽しむことができる機会を、検定という手法を用いて広くみなさまに提供しています。 数学検定は、 数学の知識をどれだけ覚えているかを問うものではありません。 数学検定の 正式名称は先に記したとおり実用数学技能検定で、社会や日常生活で数学がいかに使える か、使われているかを、検定問題を通じて理解いただくことに重きを置いております。数学 を理解し、使えるようになるということは、金融・情報・AI・工学・技術・流通・サービ スなど、 文系理系を問わず、 さまざまな分野の発展に寄与する人材の育成につながります。 また、数学的に考えることによって、他者との情報・意見交換が正確に行えるようになると いうことは、社会の中でとくに役立つ技能となります。 当協会が、 なぜ発足当初から記述式の答案を大切にしてきたかは、 数学検定のあり方と直 接かかわると同時に、 数学という学問をいかに捉えるかに応えることとも関連します。 数学 的に考えることは人類にとって基本的な思考方法であり、この思考方法が存在することに
- 36 -
�
- ▲TOP

- ページ: 41
- よって人類は社会を構築してきたといっても過言ではありません。 数学の学びを通して、 知識や技能を習得するだけでなく、 それらを活用して問題を解決し たり、新しい知識や技能を導き出したりする過程で、 「考える」ことの質を高めていくこと が大切です。このため、記述することは必要不可欠であると考えています。 記述式を重んじる理由 (1) 条件から結論を導くための筋道を記述することによって、情報を整理し、条件を導き出 し、正確に伝える力を身に付けることができます。 (2) 考えたこと、その過程や結果を記述することによって、考えがどこまで到達したかを確 認でき、よりよい考えや説明の仕方を導くきっかけをみつけることができます。 (3) 考え方を記述し振り返ることにより、数学的な考え方は一通りではないことが分かり、 社会のさまざまな問題を解決する場合にも考え方は1つではないことが理解でき、 物事 を多面的に見る力を高めることができます。 (4) 新しい知識や技能を導く過程で、その意味や手順を記述することによって、それらの知 識・技能をよりよく習得することができます。 (5) 自らの考えを記述して第三者に伝えることは、社会生活においても重要なことであり、 数学の学びを通してその基礎的な技能を身につけることができます。
数学が出来る人はこんな答案を書いています 【問題1】準2級2次:数理技能検定(2次関数のグラフと x 軸の共有点)
【答案1】 (東京都 中学3年女子)
- 37 -
�
- ▲TOP

- ページ: 42
- 【答案2】 (岐阜県 高校1年男子)
コメント 答案1は、放物線が x 軸と異なる2点で交わるのは頂点の y 座標が負であることを用い ている。これは放物線と x 軸との位置関係を幾何学的に捉えたものである。答案2は、判別 式が正となることに着目している。 これは、 放物線の式を2次方程式と関連付けて代数的に 解いたものである。 数学の問題へのアプローチの仕方は、一通りでないことを示している。このことは、社会 のさまざまな問題を解決する方法が一通りでないことを理解することに通じる。 【模範解答】
- 38 -
�
- ▲TOP

- ページ: 43
- 【問題2】2級2次:数理技能検定(確率:場合分け)
【答案】 (福岡県 高校2年男子)
コメント この問題のポイントは、さいころを6回振ったときに動点Pが頂点Aにある目の出方が 1通りでないことにある。上記の答案は、題意に合う目の出方の場合分けが的確で、式も見 やすく簡潔に書かれている。採点者に受検者の考えが正確に伝わる答案である。 社会生活においても、 第三者に自分の考えを筋道立てて正確に伝えることは、 とても重要 なことであり、数学の学びがこのような習慣を身に付けるために役立つことを示している。
- 39 -
�
- ▲TOP

- ページ: 44
- 【模範解答】
【問題3】2級2次:数理技能検定(積分:放物線で囲まれた図形の面積)
【答案】 (大阪府 高校2年女子)
- 40 -
�
- ▲TOP

- ページ: 45
- コメント 2つの放物線で囲まれた部分の面積を求める式を立てるために、図を用いて説明してい る。 この問題の解答として図を描くことは必須ではないが、 図を描くことによって考えが正 しいことを自ら確認でき、正確な結論を導くことにつながっている。 図と式を用いることで、情報を整理し、定着させることができる。これは、数学的な考え 方を養うことで物事を多面的に見る力が身に付くことを示している。 【模範解答】
- 41 -
�
- ▲TOP

- ページ: 47
- 飯高先生の数学講座
昨年度に引き続き、2018 年度も4回にわたって飯高先生の数学講座を開講した。参加者 の多くは社会人であるが、 小学生、 中学生及び高校生また年配の方の参加が定着している。 講座の内容は高等学校で履修する数学を前提とした高度なものであるが、受講者の理解度、 満足度は高く、毎回生涯学習として数学を楽しんでいる様子が伝わってくる。 第 21 回 2018.05.19「古代エジプトの分数計算を学ぶ」 ・講座のねらい 古代エジプトの分数計算の仕組みを学び現代の数学教育へ活かす。数学の歴史は古 く、4000 年前から数学で苦労してきた歴史から学ぶことが多い。 ・内容 1.古代エジプトの数字 2.単位分数の表示 4.現代でも解決できない分数の難問 ・受講者数 17 人(未就学児1人、中学生1人、高校生2人を含む) 第 22 回 2018.09.01「円錐曲線の極と極線」 ・講座のねらい 2次曲線の性質を円錐曲線の極と極線の理論を元に一般的に調べる。射影平面を考 えて一般化すると、 極と極線がよくわかる。 これは受験数学の根本の理解につながる。 ・内容 1.放物線の部分の面積計算 2.円に対する極と極線 3.同次座標と無限遠点 4.射影2次曲線 ・受講者数 25 人(小学生2人、中学生2人を含む) 第 23 回 2018.11.10「放物線をあらためて考える」 ・講座のねらい 学習指導要領の縛りがあり数学 II の入試問題には放物線の面積を求める問題しか出 せない。 これでは入試問題を作る上で大きな制約である。 しかし極と極線の理論を知る とたくさん作る術がわかる。このように一歩進んだ立場で放物線をあらためて考える。 これは教育の現場で有用な見方を提供できると思う。 ・内容 1. 放物線と極線 2 本の囲む面積 2. 放物線の極と極線 3. 放物線と極線の作る調和点列 4. 放物線と極線の作る調和点列(一般の場合) ・受講者数 28 人(小学生 1 人、高校生 6 人を含む) 3.パピルス文書にある分数計算
- 42 -
�
- ▲TOP

- ページ: 48
- 第 24 回 2019.03.09「無限遠点と射影 2 次曲線」 ・講座のねらい 円錐曲線での極と曲線を理解するには無限遠点を考慮する必要がある。円錐曲線と 極線の持つ調和点列の性質を射影 2 次曲線で考えると複雑な計算がいらない。 ・内容 1.平面に無限遠点を付け加えて射影平面を作る 2.同次座標を導入する 3.射影 2 次曲線の極と極線の関係 4.調和点列の性質の簡単な証明 ・受講者数 30 人(小学生3人、高校生2人を含む)
- 43 -
�
- ▲TOP

- ページ: 49
- 研究機関の指定について
平成 27 年(2015 年)10 月 1 日 公益財団法人日本数学検定協会内に学習数学研究所開設準備室が設立された。日本学 術振興会の科学研究費助成事業(科研費)に応募するために、学習数学研究所が文部科学 大臣から学術研究機関(研究機関)の指定を受けることが必要である。そのため、学習数 学研究所の規程類を作成する等、研究所としての体制を整える作業に取り掛かった。 平成 28 年(2016 年)1 月 16 日 理事会で、平成 28 年(2016 年)2 月 1 日付けで学習数学研究所を開設することが承認 された。 平成 28 年(2016 年)2 月 1 日 学習数学研究所が開設された。 平成 28 年(2016 年)2 月 29 日 検定問題品質委員の松嵜昭雄先生 (埼玉大学) 、 塩澤友樹先生 (小石川中等教育学校 (当 時) )を特任研究員として招聘した。 平成 28 年(2016 年)4 月 8 日 申請書及び添付資料一式を文部科学省研究振興局学術研究助成課企画室に仮提出し た。 平成 28 年(2016 年)6 月 1 日 この日以降、文部科学省からの指摘とそれに対する修正を数度繰り返した。 平成 29 年(2017 年)4 月 年度が変わったため申請書類一式を改めて提出した。 平成 29 年(2017 年)8 月 31 日 文部科学省より、科学研究費補助金取扱規程(昭和 40 年 3 月 30 日文部省告示第 110 号)第 2 条第 1 項第 4 号に規定する研究機関に指定された。 指定後、e-Rad(府省共通研究開発管理システム)に研究者を登録し、科学研究費に 応募する体制が整った。
- 44 -
�
- ▲TOP
- ページ: 50
- 文部科学省認定「高校生のための学びの基礎診断」測定ツール
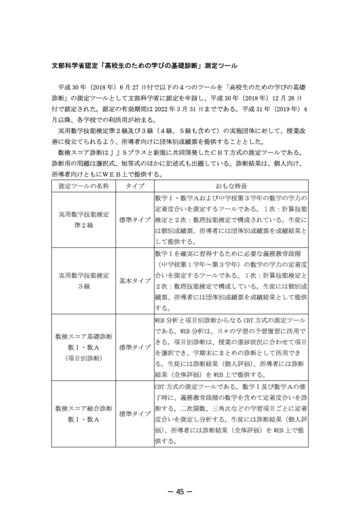
平成 30 年(2018 年)6 月 27 日付で以下の4つのツールを「高校生のための学びの基礎 診断」の測定ツールとして文部科学省に認定を申請し、平成 30 年(2018 年)12 月 26 日 付で認定された。認定の有効期間は 2022 年 3 月 31 日までである。平成 31 年(2019 年)4 月以降、各学校での利活用が始まる。 実用数学技能検定準2級及び3級(4級、5級も含めて)の実施団体に対して、授業改 善に役立てられるよう、指導者向けに団体別成績票を提供することとした。 数検スコア診断はJJSプラスと新規に共同開発したCBT方式の測定ツールである。 診断用の問題は選択式、短答式のほかに記述式も出題している。診断結果は、個人向け、 指導者向けともにWEB上で提供する。 測定ツールの名称 タイプ おもな特長 数学Ⅰ・数学Aおよび中学校第3学年の数学の学力の 実用数学技能検定 準2級 定着度合いを測定するツールである。1次:計算技能 標準タイプ 検定と2次:数理技能検定で構成されている。生徒に は個別成績票、指導者には団体別成績票を成績結果と して提供する。 数学Ⅰを確実に習得するために必要な義務教育段階 (中学校第1学年~第3学年)の数学の学力の定着度 実用数学技能検定 3級 基本タイプ 合いを測定するツールである。1次:計算技能検定と 2次:数理技能検定で構成している。生徒には個別成 績票、指導者には団体別成績票を成績結果として提供 する。 WEB 分析と項目別診断からなる CBT 方式の測定ツール 数検スコア基礎診断 数Ⅰ・数A (項目別診断) 標準タイプ である。WEB 分析は、日々の学習の予習復習に活用で きる。項目別診断は、授業の進捗状況に合わせて項目 を選択でき、学期末にまとめの診断として活用でき る。生徒には診断結果(個人評価) 、指導者には診断 結果(全体評価)を WEB 上で提供する。 CBT 方式の測定ツールである。数学Ⅰ及び数学Aの修 了時に、義務教育段階の数学を含めて定着度合いを診 数検スコア総合診断 数Ⅰ・数A 標準タイプ 断する。二次関数、三角比などの学習項目ごとに定着 度合いを測定し分析する。生徒には診断結果(個人評 価) 、指導者には診断結果(全体評価)を WEB 上で提 供する。
- 45 -
�
- ▲TOP

- ページ: 51
- 免許状更新講習
平成 31 年(2019 年)2 月 22 日付けで、文部科学省総合教育政策局教育人材政策課に免 許状更新講習(選択領域講習)の開設者の指定を申請し、平成 31 年(2019 年)3 月 8 日 付けで指定された。 平成 31 年(2019 年)3 月 13 日付けで、教職員支援機構 次世代教育推進センター更新 講習認定係に免許状更新講習の認定を申請した。 平成 31 年(2019 年)9 月 8 日(日)、9 月 22 日(日)、9 月 29 日(日)フォーラムエ イト(渋谷区)での開講を予定している。講師は清水理事長と渡邉理事が担当する。 開講日 講習の名称 平成 31 年(2019 年)9 月 8 日(日) 【選択】これからの算数・数学教育(小学校算数科を中心に) 小学校算数科にかかわる内容を中心に、つぎの構成で講習を実施す る。
1.平成期の学習指導要領改訂の変遷 2.平成期の小学校学習指導要領の改訂と算数科 3.算数科における問題発見とその解決(具体例を通して) 4.算数科における主体的・対話的で深い学びの実現 ((1)背景・考え方) 5.算数科における主体的・対話的で深い学びの実現 ((2)授業づくり・学習評価) 6.算数科における主体的・対話的で深い学びの実現((3)模擬授業) 清水 静海 小学校教諭、数学科教諭(中学校・義務教育学校・高等学校・中等教育 学校・特別支援学校) 30人 平成 31 年(2019 年)9 月 22 日(日) 【選択】これからの算数・数学教育(CAI の活用を中心に) 算数・数学において現在は情報機器活用はほとんど行われていません。 将来の算数・数学での授業の目標は計算技能から創造性の育成へと変 わります。このような変化の時代において先生方が情報機器を使うこ とを経験することは重要と考えます。講義では各自が情報機器を手に とって実際に使うことを経験し、創造的な算数・数学の思考方法を学び ます。また、授業においては算数・数学の活用を具体的に進めることが できるような訓練を行います。Work Shop 方式を活用します(情報機器 はこちらで用意します) 。 渡邉 信 小学校教諭、数学科教諭(中学校・義務教育学校・高等学校・中等教育 学校・特別支援学校) 30人
講習の概要
担当講師 主な受講対象者 定員 開講日 講習の名称
講習の概要
担当講師 主な受講対象者 定員
- 46 -
�
- ▲TOP

- ページ: 52
- 開講日 講習の名称
平成 31 年(2019 年)9 月 29 日(日) 【選択】これからの算数・数学教育(中学校数学科を中心に) 中学校数学科にかかわる内容を中心に、つぎの構成で講習を実施しま す。
1.平成期の学習指導要領改訂の変遷 2.平成期の中高等学校学習指導要領の改訂と数学科 3.数学科における問題発見とその解決(具体例を通して) 4.数学科における主体的・対話的で深い学びの実現 ((1)背景・考え方) 5.数学科における主体的・対話的で深い学びの実現 ((2)授業づくり・学習評価) 6.数学科における主体的・対話的で深い学びの実現((3)模擬授業) 清水 静海 小学校教諭、数学科教諭(中学校・義務教育学校・高等学校・中等教育 学校・特別支援学校) 30人
講習の概要
担当講師 主な受講対象者 定員
- 47 -
�
- ▲TOP
- ページ: 53
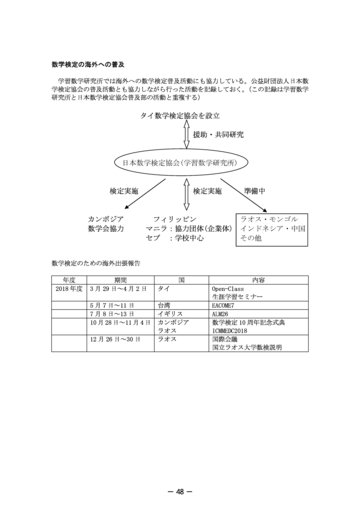
- 数学検定の海外への普及
学習数学研究所では海外への数学検定普及活動にも協力している。公益財団法人日本数 学検定協会の普及活動とも協力しながら行った活動を記録しておく。 (この記録は学習数学 研究所と日本数学検定協会普及部の活動と重複する)
タイ数学検定協会を設立 援助・共同研究
日本数学検定協会(学習数学研究所)
検定実施
検定実施
準備中
カンボジア 数学会協力
フィリッピン マニラ:協力団体(企業体) セブ :学校中心
ラオス・モンゴル インドネシア・中国 その他
数学検定のための海外出張報告 年度 2018 年度 期間 3 月 29 日~4 月 2 日 5 月7日~11 日 7 月 8 日~13 日 10 月 28 日~11 月 4 日 12 月 26 日~30 日 国 タイ 台湾 イギリス カンボジア ラオス ラオス 内容 Open-Class 生涯学習セミナー EACOME7 ALM26 数学検定 10 周年記念式典 ICMMEDC2018 国際会議 国立ラオス大学数検説明
- 48 -
�
- ▲TOP

- ページ: 54
- 出版
①森北出版 『完全ガイド! 数学検定 1 級 出題パターン徹底研究』 2018.12.12 発行。 ②日本実業出版 『ビジネスで使いこなす「定量・定性分析」大全』 「ビジネスで使いこなす入門定量分析」(2008 年発行)、「ビジネスで使いこなす入 門定性分析」(2009 年発行)の合本。 2019.01.20 発行。
学習支援
2018年度は小学校・中学校計11校で算数・数学の学習指導を行った。 葛飾区立柴又小学校、葛飾区立中青戸小学校、葛飾区立葛飾小学校、 葛飾区立北野小学校、葛飾区立水元中学校、葛飾区立中川中学校、 葛飾区立金町中学校、足立区立皿沼小学校、文京区立第八中学校、 文京区立第九中学校、文京区立第十中学校
- 49 -
�
- ▲TOP

- ページ: 55
- イベントの実施
2018.04.03(火)学びのフェス 2018 春(科学技術館、主催:毎日新聞社、毎日小学生新聞) 「ストローで立体を作ろう!」 正四面体、正八面体、 (正六面体)の制作指導をした。 参加者:小学生 72 人、来場者:1500 人(保護者を含む) 2018.08.08(水) 「算数トライアスロン」 (さいたま市教育委員会 生涯学習センター 植竹公民館) 算数パズル、ミニ検定を実施した。 参加者:小学生 41 人 2018.08.22(水)学びのフェス 2018 夏(科学技術館、主催:毎日新聞社、毎日小学生新聞) 「算数トライアスロン」 円かき、算数パズル、ミニ検定を実施した。 参加者:小学生 72 人、来場者:1800 人(保護者を含む) 2018.12.21(金) 「算数トライアスロン」 (足立区立皿沼小学校) 2019.02.12(火)チャレンジセミナー (主催:墨東特別支援学校いるか分教室、会場:国立がん研究センター中央病院) 「ストローとモールで立体を作ろう」 正二十面体の制作指導をした。 参加者:小学生 3人、中高生 5人 2019.03.30(土)こどもめばえフェスタ (主催:日本ドリコム、後援:日本数学検定協会、会場:3331Arts Chiyoda) 「算数検定 ミニ検定」 来場者:1973 人(幼児・小学生 1093 人)
- 50 -
�
- ▲TOP

- ページ: 57
- 学習数学研究所運営会議 議事録
日時:2018 年 12 月 12 日(水)16:30~18:30 場所:会議室(8人掛け) 出席者:清水、渡邉、中村、松本 第1号議案 運営会議の件 定例会議では、 次年度の事業計画及び予算について検討し、 当該年度の事業及び決算を承 認することが提案され、審議の結果、全会一致で承認された。 第2号議案 免許状更新講習の件 免許状更新講習を開設することが提案され、審議の結果、全会一致で承認された。選択領 域の講座を平成 31 年度中に開設できるよう、準備を進める。 講師としての有資格者を検定問題品質委員等からリストアップする。 事業報告1.検定問題品質会議の件 2019 年2月3日(日)全体会・分科会(幼小中部会・高大部会)及び情報交換会を開催す る。全体会の講演は、渡邉理事と中村研究員が行う。 8月頃に小学校・中学校の若手委員を招集して、小委員会を開催し、作成した問題につい て検討する。 事業報告2.高校生のための学びの基礎診断の件 文部科学省に「高校生のための学びの基礎診断」の測定ツールとして、以下の4点を申請 した。現在認定審査中で、認定の公表(10 月~11 月予定)が遅れている。 ・実用数学技能検定 準2級 ・実用数学技能検定 3級 ・数検スコア総合診断 数Ⅰ・数A ・数検スコア基礎診断 数Ⅰ・数A(項目別診断) 事業報告3.検定問題等検討会の件 毎月1回検定問題等検討会を開催し、 検定問題を中心として、 全国学力調査の調査問題、 大学入学共通テストプレテストの問題、数学教育等について検討している。 事業報告4.数学講座の件 飯高先生の数学講座を引き継ぎ、来年度から桑田孝泰教授(東海大学情報数理学科)の数 学講座を開設し、年4回実施する。 数学講座が、才能ある児童・生徒のための高度な数学学習の場となるよう、講師を充実さ
- 51 -
�
- ▲TOP

- ページ: 58
- せ、実施回数を増やすこと等が考えられる。 事業報告5.算数・数学イベントの件 小学生を対象としたイベントを開催し、算数・数学の楽しさを伝えた。 2018.04.03 学びのフェス 2018 春(科学技術館、主催:毎日新聞社、毎日小学生新聞) 2018.08.22 学びのフェス 2018 夏(科学技術館、主催:毎日新聞社、毎日小学生新聞) 事業報告6.学習支援の件 現在、小学校・中学校合わせて 10 校程度で学習支援を行っている。目的は、算数・数学 への興味関心を高める、検定実施前の数学力向上等が挙げられる。 現在実施している講座に関しては、要請があれば今後も続けていく。 事業報告7.出版の件 森北出版から「完全ガイド!数学検定1級 出題パターン徹底研究」を出版した。
- 52 -
�
- ▲TOP

- ページ: 59
- 検定問題品質会議
日時:2019 年 2 月 3 日(日)13 時 30 分~20 時 場所:文昌堂ビル 10階会議室、6階リフレッシュエリア 1.全体会(10階会議室) (1)理事長挨拶 清水静海理事長(帝京大学教授) (2)新委員紹介 大石隆(世田谷学園中学校・高等学校) , 中嶋亮(板橋区立加賀中学校) ,上田大悟(台東区立御徒町台東中学校) 粕川真紀(日本数学検定協会) ,永尾憲一(日本数学検定協会) (3)講演 中村力「数学と理科の融合」 渡邉信「問題作成へのお願い」 (4)全体会のまとめ 渡邉信常務理事 2.分科会 検定問題品質委員が作成した問題を各自紹介し、内容を検討した。 ・幼児・小中部会(10階会議室) 幼児関係1人、小学校5人、中学校6人、協会関係8人 ・高大部会(6階リフレッシュエリア) 高等学校5人、大学7人、協会関係6人 3.情報交換会(10階会議室) 幼児関係1人、小学校5人、中学校3人、高等学校5人、大学7人、 協会関係15人
- 53 -
�
- ▲TOP

- ページ: 60
- 検定問題等検討会
2018.04.25(第6回) 「数学の科学&工学領域への適用(応用)と大学・高校の数学との関連」 「2月検定3級及び4級について」 2018.05.23(第7回) 「数学検定論述問題(記述式問題)準2級及び3級の得点分布」 「数学知識の定着について」 2018.06.20(第8回) 「数学コーチャー研究発表会・研修会 模擬授業・ロールプレイングについて」 2018.07.17(第9回) 「算数検定記述式答案の誤答分析-除法-」「数学用語の変更と問題点」 2018.08.28(第 10 回) 「全国学力・学習状況調査 小学校算数」「いろいろな解法について」 2018.09.19(第 11 回) 「高校物理と数学との関連」「数学不要論に対する対応」 参加者 渡邉、松本、中村、山口、永尾 2018.10.16(第 12 回) 「数学検定の問題と数値」「表を作る・グラフを描くことの目的は?」 「検定問題作成時の資料について」 参加者 渡邉、松本、中村、藤原 2018.11.13(第 13 回) 「これは記述式と言えるか?」「正答率と合格率の関係(3級~5級)」 参加者 渡邉、松本、中村、穂積、大村 2018.12.12(第 14 回 12/12) 「高校理科と数学との関係」「校正の失敗」 参加者 渡邉、松本、中村、山口、上林 2019.01.22(第 15 回) 「大学入試センター試験 数学Ⅰ・数学A 統計の問題について」 参加者 渡邉、松本、中村、山口、上林、永尾 2019.02.20(第 16 回) 「問題を作るということ」 参加者 渡邉、松本、中村、水原、山口 2019.03.27(第 17 回) 「この答えをいかに扱うか?」「日常事象の数理化の大切さ(消費税)について」
- 54 -
�
- ▲TOP

- ページ: 61
- 第6回検定問題等検討会(2018.4.25)
線形代数の応用性調査(メモ)
1.線形代数の特質 線型方程式とは、線型性を持つ写像(関数・作用素)の等式で表される方程式のことで、 線型方程式においては、その線型性から解の重ね合わせが成り立つなどいくつものよい性 質が成り立つ。線型方程式(特に多変数の一次代数方程式 i.e.連立1次方程式)の研究か ら行列などの手法が整備され、線型代数学という一分野が形成された。物理学や工学で多 用される線形微分方程式にも、線形代数のコンセプトや手法が非常に多く適用されている。 さらに、統計学や線形方程式のプログラミングによる数値的解法にも行列を用いたエレガ ントな解法が多く開発されている。
◎線形方程式(1次方程式)
⇔
ax b
⇒
解x
b (a 0 ) a
◎連立方程式
a11 x1 a12 x 2 a1n x n b1
a 21 x1 a 22 x 2 a 2n x n b2
アナロジー
⇔ :
a n1x1 a n 2x 2 a nn x n bn
A x =b
⇒
解 x = A1 b ( A ≠0 )
a1n a11 a12 x1 b1 a 2n a a b2 x2 , = 、 = A = 21 22 b x b x a a ann n2 n n n1
アナロジー とおけば
◎連立線形微分方程式
a11 (x )y1 a12 (x )y2 a1n (x )yn r1 (x ) y1 a21 (x )y1 a22 (x )y2 a2n (x )yn r2 (x ) y2
dY AY R dt
:
:
:
⇔
an1 (x )y1 an 2 (x )y2 a2n (x )yn rn (x ) yn
a11 (x ) a12 (x ) a1n (x ) r1 (x ) y1 a 21 (x ) a 22 (x ) a 2n (x ) r2 (x ) y2 A= ,y = ,R = y r (x ) a (x ) a (x ) a ( x ) n n2 nn n n1
とおけば
- 55 -
�
- ▲TOP
- ページ: 62
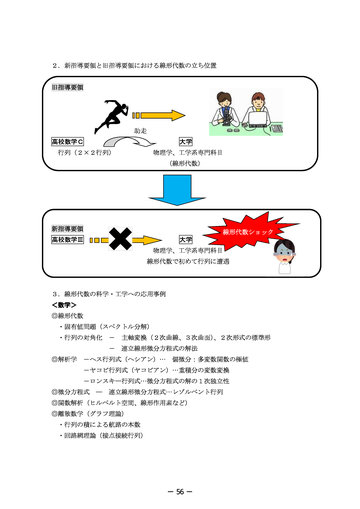
- 2.新指導要領と旧指導要領における線形代数の立ち位置 旧指導要領
助走 高校数学C 行列(2×2行列) 大学 物理学、工学系専門科目 (線形代数)
新指導要領 高校数学Ⅲ 大学
線形代数ショック 物理学、工学系専門科目 線形代数で初めて行列に遭遇
3.線形代数の科学・工学への応用事例 <数学> ◎線形代数 ・固有値問題(スペクトル分解) ・行列の対角化 - 主軸変換(2次曲線、3次曲面) 、2次形式の標準形 - 連立線形微分方程式の解法 ◎解析学 -ヘス行列式(ヘシアン)… 偏微分:多変数関数の極値 -ヤコビ行列式(ヤコビアン)…重積分の変数変換 -ロンスキー行列式…微分方程式の解の1次独立性 ◎微分方程式 ― 連立線形微分方程式…レゾルベント行列 ◎関数解析(ヒルベルト空間、線形作用素など) ◎離散数学(グラフ理論) ・行列の積による航路の本数 ・回路網理論(接点接続行列)
- 56 -
�
- ▲TOP

- ページ: 63
- ◎統計学(多変量解析) ・最小2乗法-回帰直線、回帰曲線による曲線あてはめ(Curve ・主成分分析 ・主因子分析 <物理学> ・古典力学-連成振動、慣性モーメント(テンソル) ・電磁気学-キルヒホッフの法則、4端子回路 ・相対論-テンソル計算(ローレンツ変換、アインシュタイン方程式) ・量子力学-シュレーディンガ-方程式井戸型ポテンシャルのエネルギー順位 -物理量の行列表現、 、交換関係、スピノール、パウリ行列 -行列力学(by ハイゼンベルグ) 、摂動法、スレーター行列式 <工学> ◎機械力学(振動) ・ロボット工学・制御工学 ・ロボットマニピュレータ-順運動学・逆運動学、特異姿勢 ・リンク機構-特異値分解による行列の階数と線形方程式の解構造の分析 ・人工衛星の軌道計算―ベクトル外積の応用 ・連成振動、多自由度振動系-固有振動数、振動モード解析 ・リアプノフの安定定理―システムの安定度判定 ・有限要素法&境界要素法―微分方程式、積分方程式の数値解法、近似解法 ◎材料力学、構造力学 ・応力とひずみ、テンソル ・モールの応力円―材料における応力(stress)解析 ◎CG(コンピュータグラフィックス), 画像解析 ・画像・ベクトルの 拡大(縮小)や回転 ―アフィン変換 ・レイトレーシング(光線追跡法) ・CG キャラクタをデザインする細分割モデリング(カトマル-クラーク細分割曲面) ・画像ひずみの修正―ステレオ解析による流体速度(3成分)の算出 ・高速フーリエ変換(FFT) ・ウェーブレット変換 ◎情報理論・通信工学 ・マルコフ連鎖-遷移確率行列 ・線形符号理論(パリティ検査符号)-生成行列、検査行列 ・アダマール行列の応用 fitting)
- 57 -
�
- ▲TOP

- ページ: 64
- <金融工学> ・CAPM、ファクターモデル <経済学> ・投入産出分析、レオンチェフ行列、ホーキンズ・サイモンの条件 (中村 力)
- 58 -
�
- ▲TOP

- ページ: 65
- 第7回検定問題等検討会(2018.5.23)
数学知識の定着について
π=3.14 はよく知っている 次の右図において円周と直線とはどちらが 長いですか? (コメントこの問題で考えることなくすぐに円 周と答えることを予想していたが、答えられなかった) 円周角の問題
科学館の学芸員(物理担当)からの話 円周角の定理は、実生活ではほとん ど使う機会がないなあと思いました。 原因のひとつは、三角関数や微分方程 式などと違い、ほとんど物理の問題に 顔を出さないからなのかもしれませ ん。 それを言ったら、 二次方程式だって そうなのかもしれませんが。 しかし、興味深い実験ではありました。 コメント 数学は主要教科として一生懸命に学んでいるが、 その知識の定着が悪すぎる。 数学を学ぶ ということの意味を考えなくてはいけないのかもしれない。 πの値が 3.14 ということは知っている。しかし、円周率の意味は分からない。 また、 円周角はほとんど知らない。 円周と聞いて円周率と間違えるためかπのことと混同す る。円周角の美しさに感動することはないならば、今回の実験の意味を理解する以前に、数 学から離れていってしまう。 (渡辺信)
- 59 -
�
- ▲TOP

- ページ: 66
- 第8回検定問題等検討会(2018.6.20)
数学コーチャーの問題について
(1)計算か直感か 極限の値を求める問題で, 高校生の計算力はすごい. あまり褒められることではないが, なんでも計算をしようとすることは悪いことではない. 次の極限値を求めなさい.
n
n
n n
n
n
n
n n
=
n
n
n n
n n
n n
n
n
=
= しかし,この問題は分母分子を√n で割れば答えは簡単に求まる.この問題は計算だけで
簡単に求めることが出来る.計算などをする必要はない.問題をよく見ると n の係数がす べて同じのときはどうなるのであろうかという問題を見つけることが出来る. 4 通りの問題 があることが分かる.
n +3+ n +4
n
n +2+ n +5
=1
この極限の値を求めることは関数の Order の問題で, 答えが1になることは見えている. 次の 3 つの極限値はグラフ電卓では求まらない.
n +3- n +4
n
n +2- n +5 n +3- n +4
n
n +2+ n +5
=0
n +3+ n +4
n
n +2- n +5
=∞
しかし,両方の符号が一致しているときは有理化をすることで求められる.ここでは, Technology よりも計算を紙に書いたほうがよい例にも見えるが,何をするかの問題発見に は,Technology が役立っている.問題を発見したときに数学はおもしろいと思う.
- 60 -
�
- ▲TOP
- ページ: 67
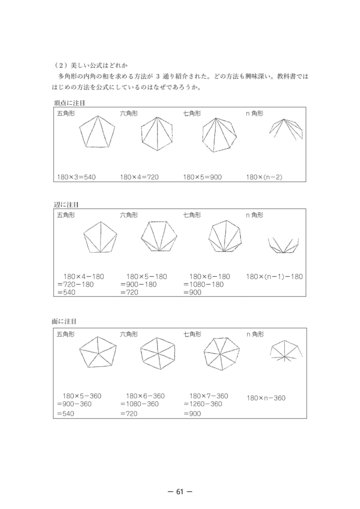
- (2)美しい公式はどれか 多角形の内角の和を求める方法が 3 通り紹介された。どの方法も興味深い。教科書では はじめの方法を公式にしているのはなぜであろうか。
- 61 -
�
- ▲TOP

- ページ: 68
- (3)用語の問題 四角形の形 四角形の定義:4 本の直線で囲まれている形 一般の四角形 一 組の辺が平行 一 直角 一 台形 向かい合う辺が平行 一 平行四辺形 長方形 (渡辺信) 辺の長さが等しい 一 正方形
- 62 -
�
- ▲TOP

- ページ: 69
- 第 9 回検定問題等検討会(2018.7.17)
数学用語の変更と問題点
1.方程式の「解」 方程式の根 root が解に変わった段階から用語の解釈が変わった。この問題はもう解決済 みなのかもしれないが確認をしたい。 2 次方程式 (x-1)2=0 の解は x=1 である。 以前はこの根x=1は重根として 2 個と数えた 代数学の基本定理である 「n次方程式の解はn個」 に対して、2 次方程式 (x-1)2=0 の 解は x=1 の 1 個は言葉の上で問題があるのではないかと思う。 数学検定では回答は「2 次方程式 (x-1)2=0 の解は x=1 である」を用いている。 この問題と似てくることが「接点」の扱いではないか。 (1) 円の接線の定義は半径と直交する点であるならば1点である。 割線と円との交点2点が限りなく近づく点としたときには2点が存在する。 (2) 曲線に対する接線を考えるときは、 (a.f(a))と (a+h.f(a+h))の2点の平均変 化率 このときも2点を考えている。 (3) x軸上での接点はこの点を2回通るとしたときに意味があう。 二つの曲線の「共有点」と言う言葉によって接点は1個と数えている。 判別式 D=0のとき の共有点は1点である。次の問題では共有点をどのように数えるのか? y=x3-3xとy=cとの交点の個数 c<-1のとき c=-1のとき c=1のとき 1<cのとき 2.積分定数の効用・必要性 積分の計算問題では積分定数 C を付けることになっている。不定積分であるから当然で あるが、定積分になると、計算上で入らない。この C を重視している感じがあるが、どの ように考えているのであろうか。積分定数を付けない解答の扱いは? 例えば速度 v=4で歩いたときにs=4t+cの直線群が解になるが、 初期条件が付く問 題のほうが応用的ではないか。応用するときには積分定数が必要になってくる。 また、三角関数などの答えの表現にはいろいろな表現があるので、C は必要かもしれない。 積分定数 C を必ず付けることを強調していく必要性はあるか。 (渡辺信) 1個 2個 2個 1個
-1<c<1のとき3個
- 63 -
�
- ▲TOP

- ページ: 70
- 第 13 回検定問題等検討会(2018.11.13)
これは記述式と言えるか?
11 月 11 日全国一斉にプレ・センター試験が行われた。対象は高校 3 年生、約 8 万人が受 験した。 この試験監督をした人の話では、 欠席者は 65 人中 28 名、 まったくやる気はなく、 時間の無駄であったと言う。その中で数学①(数学Ⅰ・数学 A)の記述式の問題が 3 題出題さ れた。この記述式と言う試験の方法は正しいであろうか?問題をみてどのように考えるか 検討したい。
今回は記述試験に対して自己判断表が添付された。試験終了後この記述式の問題は自己 診断をするようになっていた。 記述式は学校教育では行われていないので、 生徒がどのよう に判断するか興味がある。 結果的には、 今まで以上の暗記力を試す問題で記述式とは認めがたい。 センター試験の中 に記述式を入れる目的は何であったのかを検討してみたい。
- 64 -
�
- ▲TOP

- ページ: 71
- 注意事項と記述式の欄の大きさについて
試験問題は B5 版が使われた。 問題訂正として配布されたのは A4版 解答用紙は特別作成であった。 (渡辺信)
- 65 -
�
- ▲TOP

- ページ: 72
- 第 16 回検定問題等検討会(2019.2.20)
問題を作るということ
今回の問題 1 から 100 までの整数で、(偶数の和)-(奇数の和)を求める 問題作成の段階 (偶数の和)-(奇数の和)を求める問題 ―問題の所在・部分と全体・規則発見― このままでは易しいか難しいか分からない。 そこで(1 から 10 までの偶数の和)―(1 から 10 までの奇数の和)を求める 1から 10 までの和が 55 はよく知られている 偶数ではないことは「同じ」ではない (1 から 100までの偶数の和)―(1 から 100までの奇数の和) この問題はおもしろいかの検討 具体的に計算をすることは簡単 より簡単に計算ができないかを考える 問題として完成 1から 2nまでの和 1から 2nまでの(偶数の和)-(奇数の和)=n 1から 2nまでの(偶数の和)=n2+n 1から 2nまでの(奇数の和)=n2 ちょっと変わった式を見つける
k=n k=2n
(1 から 2nまでの偶数の個数=n)
Σ(4k-1)=Σk
k=1 k=1
より発展させる段階 1 から 100 までの整数で、(偶数の 2 乗の和)-(奇数の 2 乗の和)を求める この問題は? 1 から 100 までの整数で、(偶数の3乗の和)-(奇数の3乗の和)を求める 問題を作ることを大切にしたい 訓練よりもひらめき? (渡辺信)
- 66 -
�
- ▲TOP

- ページ: 73
- 第 17 回検定問題等検討会(2019.3.27)
この答えをいかに扱うか?
問題 1 さいころを投げて偶数の目が出る確率を求めよ(記述式であったとして) 答え 答え 答え 1/2 3/6=1/2 4/8=1/2
問題 2 直線の方程式は傾きと y 切片からできているこ とを前提にして 答え 答え y=2x y=2x+0
問題 3 正方形の 1 辺の長さ a,長方形の縦 x、横 y のとき周の長さが等しいことを式で示 せ。 答え 答え 4a=2x+2y 2a=x+y
問題 4 3.1+5.9の計算結果(すでに両方9も9.0も正しいという見解を示した) 答え 答え 答え 9 9.0 9.
問題 5 3.1mの針金と5.9mの針金を合わせたら何mか 答え 答え 答え 9m 9.0m 9.m
問題 6 10―3の計算(サクランボ方式?) 答え 答え 10の分解を (7+3)-3=7 10の分解を (3+7)-3=7 (渡辺信)
ほかにこまった答えを知っていますか?
- 67 -
�
- ▲TOP

- ページ: 74
- 問題検討会
日時:2018 年 9 月 20 日(木)17:30~18:30 場所:御徒町台東中学校 御徒町台東中学校増田校長から、検定問題品質委員として中嶋亮先生(板橋区立加賀中 学校)、上田大悟先生(台東区立御徒町台東中学校)を紹介していただき、新規作成問題 について意見交換をした。 参加者:増田、中嶋、上田、渡邉、松本
- 68 -
�
- ▲TOP

- ページ: 75
- 編集後記 公益財団法人日本数学検定協会内に学習数学研究所が設立されてから3年が経ちまし た。この間に、文部科学省から学術研究機関の指定を受け、科学研究費助成事業(科研 費)に応募できる体制が整いました。また、 「高校生のための学びの基礎診断」の測定ツ ールとして、実用数学技能検定準2級、3級及び数検スコア基礎診断数Ⅰ・数A、数検 スコア総合診断数Ⅰ・数Aが文部科学省に認定されました。文部科学省から教員の免許 状更新講習の開設者の指定を受け、2019 年9月に3つの講座を開講する予定でいます。 このように、この3年間で学習数学研究所は公的な事業を推進する機関として確立し つつあります。これからも、算数教育・数学教育に関する様々な事業を通して数学の生 涯学習の進歩発展に寄与してまいりますので、宜しくお願いいたします。 (松本 精一)
編集委員 島田 功 清水 静海 中村 力 羽中田 彩記子 松嵜 昭雄 松本 精一 渡邉 信
学習数学研究紀要 第2巻 発行日 2019 年 3 月 31 日
編集発行 公益財団法人 日本数学検定協会 学習数学研究所 所長 清水 静海 〒110-0005 東京都台東区上野 5-1-1 TEL 03-5812-8340 FAX 03-5812-8346 印刷所 サイトー印刷 株式会社
- 69 -
�
- ▲TOP
 学習数学研究紀要 創刊号(第2巻)
学習数学研究紀要 創刊号(第2巻) 学習数学研究紀要 創刊号(第2巻)
学習数学研究紀要 創刊号(第2巻)

































































