個人受検の申し込み
検定日一覧
関連書籍
検定過去問題
「数学」をあきらめない、「数学」で未来を切り開く。
検定情報
個人受検にはA日程とB日程があり、検定日や実施階級などが異なります。
個人受検A日程（年3回）
- 年3回全国で開催
- 受検「地域」選択
- 定員なし
実施階級：1～8級、かず・かたち実施
-
申込受付終了 第440回 2025年
4月13日日実施
申込受付期間 2月10日月 〜 3月4日火
-
申込受付前 第444回 2025年
7月27日日実施
申込受付期間 5月26日月 〜 6月17日火
-
申込受付前 第448回 2025年
10月26日日実施
申込受付期間 8月25日月 〜 9月17日水
ネットはもちろん、
LINEやコンビニでも申し込み可能
個人受検B日程 直近の日程
- 通年で随時開催
- 受検「会場」選択
- 定員あり
実施階級：準1～11級（検定日、会場による）
-
申込受付中 第441回 2025年
6月7日土実施
申込受付期間 4月7日月 〜 5月8日木
-
申込受付中 第442回 2025年
6月21日土実施
申込受付期間 4月21日月 〜 5月20日火
-
申込受付前 第443回 2025年
7月12日土実施
申込受付期間 5月12日月 〜 6月10日火
まずは近くの検定会場を調べてみよう
入試優遇も！特長とメリット
実用数学技能検定は文部科学省後援の検定！
「入試優遇制度」や
「単位認定制度」が
活用できます！
【入試優遇制度】
大学・短大・専門学校
全国490校以上！
【単位認定制度】
大学・高等専門学校・高等学校
全国410校以上！
※2025年1月現在。当協会調べ
大学入試において、実用数学技能検定の取得を優遇・活用する大学・短大が多数あります。入試時の点数加算や出願要件、参考要素とするなど、それぞれの大学・短大において、内容はさまざまです。
また、大学・高等専門学校・高等学校などで、一定の階級の実用数学技能検定取得者に対して、特定の科目の単位取得が認められています。
日々の学習に活用して、
数学力をアップしよう！
苦手や弱点がわかる
「個別成績票」が
発行されます！
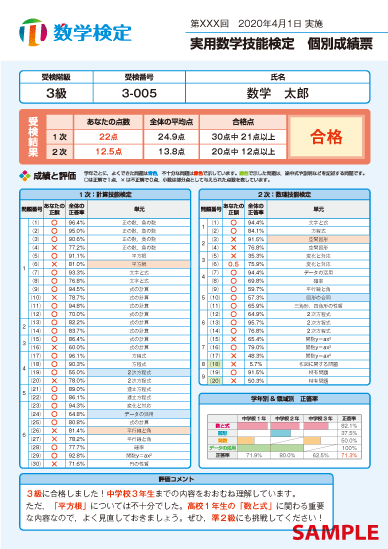
個別成績票表面
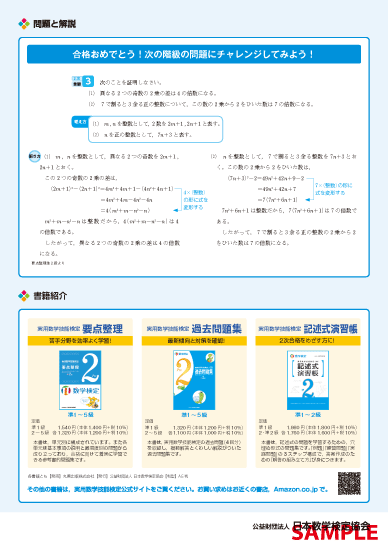
個別成績票裏面
実用数学技能検定（数学検定・算数検定）のすべての受検者の方に、受検後も引き続き算数・数学の学習に励んでいただけるよう、個別成績票を発行しています。
個別成績票には、小問ごとの成績に加え、問題の内容、結果を表すグラフ、評価コメント、成績に応じたチャレンジ問題などを掲載しています。検定結果を合否や正誤だけでとらえるのではなく、出題された内容と照らし合わせて見直すことで、今後の学習に生かすことができます。
思考力・判断力・表現力の向上に！
数学検定はすべて
「記述式」の検定です！
数理技能検定の採点例①
数理技能検定の採点例②
実用数学技能検定（数学検定・算数検定）は、計算結果のみではなく、それにいたる解法の説明や、計算式などを記述します。マークシート方式のように与えられた選択肢のなかから正解を選ぶ解答方式では評価できない理解度についても判定します。正解していなくても、途中までの考え方が正しい場合は、部分点が付与されます。
※実際の検定では、解答用紙は返却されません。
検定過去問題にチャレンジ！
準2級の解答を見る
閉じる
準1級の解答を見る
閉じる
お申し込みはこちらから
個人受検にはA日程とB日程があり、検定日や実施階級などが異なります。
個人受検A日程（年3回）
- 年3回全国で開催
- 受検「地域」選択
- 定員なし
実施階級：1～8級、かず・かたち実施
-
申込受付終了 第440回 2025年
4月13日日実施
申込受付期間 2月10日月 〜 3月4日火
-
申込受付前 第444回 2025年
7月27日日実施
申込受付期間 5月26日月 〜 6月17日火
-
申込受付前 第448回 2025年
10月26日日実施
申込受付期間 8月25日月 〜 9月17日水
ネットはもちろん、
LINEやコンビニでも申し込み可能
個人受検B日程 直近の日程
- 通年で随時開催
- 受検「会場」選択
- 定員あり
実施階級：準1～11級（検定日、会場による）
-
申込受付中 第441回 2025年
6月7日土実施
申込受付期間 4月7日月 〜 5月8日木
-
申込受付中 第442回 2025年
6月21日土実施
申込受付期間 4月21日月 〜 5月20日火
-
申込受付前 第443回 2025年
7月12日土実施
申込受付期間 5月12日月 〜 6月10日火
まずは近くの検定会場を調べてみよう
調べてみよう目安の階級
高校生の目安となる階級
![準2級]()
| 目安の学年 | 高校1年程度（数学Ⅰ・数学A程度） |
|---|---|
| 構成 | 1次：計算技能検定、2次：数理技能検定があります。 はじめて受検するときは1次・2次両方を受検します。また、1次も2次も同じ日に行います。 |
| 検定料 | 個人受検：5,600円 団体受検：4,800円 |
出題の構成
準2級についてくわしく見る
閉じる
![2級]()
| 目安の学年 | 高校2年程度（数学Ⅱ・数学B程度） |
|---|---|
| 構成 | 1次：計算技能検定、2次：数理技能検定があります。 はじめて受検するときは1次・2次両方を受検します。また、1次も2次も同じ日に行います。 |
| 検定料 | 個人受検：6,500円 団体受検：5,600円 |
出題の構成
2級についてくわしく見る
閉じる
![準1級]()
| 目安の学年 | 高校3年程度（数学Ⅲ・数学C程度） |
|---|---|
| 構成 | 1次：計算技能検定、2次：数理技能検定があります。 はじめて受検するときは1次・2次両方を受検します。また、1次も2次も同じ日に行います。 |
| 検定料 | 個人受検：7,300円 団体受検：6,400円 |
出題の構成
準1級についてくわしく見る
閉じる
めざせ合格！学習サポート
検定合格に向けた学習や
基礎的な数学力の向上に！
過去問題集や参考書、
「関連書籍」で学習しよう！
過去問題集
要点整理
過去に実際に使われた検定問題を多数収録している「実用数学技能検定 過去問題集」や、単元別に構成された参考書のような問題集で合格に向けて着実に学習できる「実用数学技能検定 要点整理」など、検定合格や基礎的な数学力の向上に向けた学習が行える、さまざまな関連書籍が発行されています。
お申し込みはこちらから
個人受検にはA日程とB日程があり、検定日や実施階級などが異なります。
個人受検A日程（年3回）
- 年3回全国で開催
- 受検「地域」選択
- 定員なし
実施階級：1～8級、かず・かたち実施
-
申込受付終了 第440回 2025年
4月13日日実施
申込受付期間 2月10日月 〜 3月4日火
-
申込受付前 第444回 2025年
7月27日日実施
申込受付期間 5月26日月 〜 6月17日火
-
申込受付前 第448回 2025年
10月26日日実施
申込受付期間 8月25日月 〜 9月17日水
ネットはもちろん、
LINEやコンビニでも申し込み可能
個人受検B日程 直近の日程
- 通年で随時開催
- 受検「会場」選択
- 定員あり
実施階級：準1～11級（検定日、会場による）
-
申込受付中 第441回 2025年
6月7日土実施
申込受付期間 4月7日月 〜 5月8日木
-
申込受付中 第442回 2025年
6月21日土実施
申込受付期間 4月21日月 〜 5月20日火
-
申込受付前 第443回 2025年
7月12日土実施
申込受付期間 5月12日月 〜 6月10日火
まずは近くの検定会場を調べてみよう
学習して良かった！合格体験記
悔しい思いをすることの意味
準2級合格
高橋 舞衣子 さん
（神奈川県・高校1年生）
準2級合格
悔しい思いをすることの意味
高橋 舞衣子 さん （神奈川県・高校1年生）
私の強み＝数学。
中学校2年生から受け続けた数検。
そのときは中学校２年生レベルの4級を受け、初挑戦だったにもかかわらず、みごと、一発で合格。続いて中学校3年生で３級を受け、結果を見るのが不安なほど不合格を覚悟したこともありました。しかし、結果を見たら圧倒的に丸の数が多く、一発とは思えないほどの好成績で合格することができました。
このまますんなりいけたなら、準2級も合格できると思っていました。ただ、現実はそう甘くはなかったです。
高校1年生の夏に準2級を受けました。検定前から不安だけの空気に包まれていました。過去問題を解いてもわからないことばかりでした。検定が始まりました。問題用紙を開いた瞬間、過去問題以上にわからない問題だらけで、心のなかで、どうせ無理と思っていました。受検の結果は……。
1次は、奇跡的に合格基準ピッタリで合格!!
2次は、あと0.5点というところで合格点に届かず…。
ほんの僅差で合格できなかったことは、すごく悔しかったです。
ただ、私はこのとき、高校の数学をまだ3か月くらいしか学習していなかったため、それにしては思っていた以上に点数が取れていて、とてもびっくりでした。
ここまでいったならあきらめたくないと思い、今回、リベンジしました。
「前回よりも点数を下げたくない！」
「僅差で不合格になりたくない！」
と思いながら、検定に挑みました。
正直、今回も不合格になるかもしれないと、覚悟はしていました。
合否を知るまでは、不安な空気に包まれていました。
ついに合否確認日となり、不合格だと思い込んでいたら、なんと…
合格でした。
後日、結果通知を受け取ったとき、点数を見てみると…10点中9点！論述式はすべて正解!! 正答率25%の問題も正解するなど、自分でもびっくりするほどの成績を残すことができました。
今回、数検受けてみて思ったのが、結果がよいことがすべてではないということです。今回合格できたのはすごくうれしいことだけど、結果を知ることよりも、自分の弱み、課題を知ることで、次へとつなげていくことが大切なことだと、あらためて実感することができました。
これを機にもっと上をめざして、2級にも挑戦したいです。
