「記述式」について
実用数学技能検定は論理構成力をみる「記述式」の検定です。「記述式」の特長や問題例・採点例をご覧になれます。
「記述式」とは
記述式は、問題の出題形式です。
記述式は、ペーパーテストで、「思考力」「判断力」「表現力」などの能力が育っているかを評価するために主として使われています。
全国学力・学習状況調査（文部科学省、平成19年度から実施）では問題形式を、選択式、短答式、記述式の3つに分類し整理しています。
当協会では、上記の短答式と記述式を合わせて「記述式」と捉えています。そして、記述式の問題を、論理読解力を問う問題と論理構成力を問う問題に分け、後者の論理構成力を問う問題をとくに論述式の問題として出題しています。
出題形式と「記述式」の分類
選択式
- 複数の選択肢から正しいものを選択する。
短答式
- 数値や用語など主として単語で答える。
記述式
- 事柄について文や図・表・グラフなどで説明する。
論理読解力
- 解法が示された問題に対して
その筋書きを読み取って答える力
論理構成力
- 解法が示されていない問題に対して
自分で筋書きをつくって答える力（論述式）
「記述式」
論述式の問題では、受検者は自由な発想で問題と向き合い、事象を数理的に捉え、数学の問題を見出し、問題を自立的に解決することが可能です。
したがって、論述式の問題では複数の解法が生じることがあり、採点では、解答の結果だけではなく、解法に応じてその過程についても的確に評価し正解としています。
たとえば、結果が合っていなくても、途中までの考え方が数学的に正しければ部分点を付与し、結果が合っているか合っていないかだけで評価するのではなく、より細やかな評価をしています。考え方が正しくない解答に対しては、たとえ結果が合っていても、不正解とすることがあります。
当協会では、「思考力」「判断力」「表現力」を、より的確に評価するためには、論理構成力を問う記述式の問題、すなわち論述式の問題による評価が必要であると考え、論述式の問題を一貫して出題しています。
「記述式」のほか、実用数学技能検定を中心とした研究および調査については、下記のリンク先でご確認ください。
数学検定の問題例・採点例
数学検定準2級
2次：数理技能検定の問題例
論述式の問題が出題されます。「解答が合っているか」だけでなく、「解答を導く過程」を記述できるかも重要です。
数学検定準2級
2次：数理技能検定の採点例
式の立て方から考え方、計算ミスや単位ミスまでていねいにチェックします。答えは正解でなくても途中まで正しく考えられていた場合は、部分点がつきます。
証明問題や作図では、解答の手順を1つひとつ確認しています。
※実際の検定では、解答用紙は返却されません。
算数検定の問題例・採点例
算数検定8級の問題例
式を立てたり、答えを出すまでの説明を書く問題も出ます。どのように考えたのか、わかりやすく伝えられることが大切です。
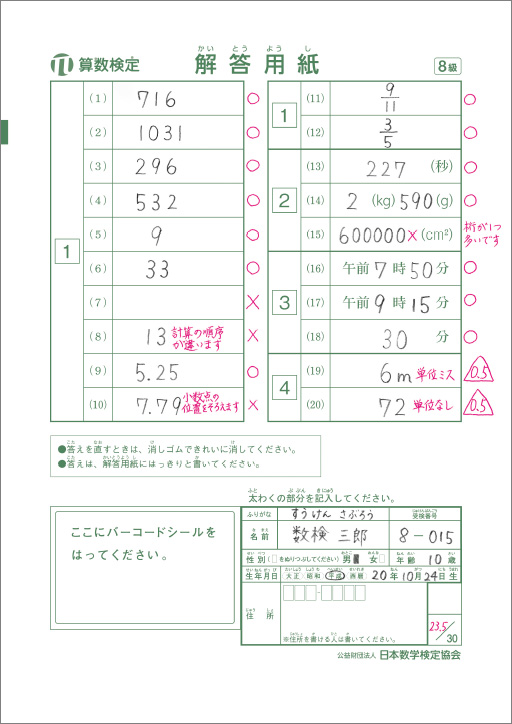
算数検定8級の採点例
式の立て方から考え方、計算ミスや単位ミスまでていねいにチェックします。答えは正解でなくても、途中まで数学的に正しく考えられていた場合は、部分点がつきます。
※実際の検定では、解答用紙は返却されません。
