書籍に関するお詫びと訂正

当協会が発行した書籍に関するお詫びと訂正をご覧になれます。

実用数学技能検定　過去問題集

実用数学技能検定　
過去問題集　数学検定準2級（2014年2月10日初版発行）

2014年2月10日に発売いたしました「実用数学技能検定　過去問題集　数学検定準2級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
別冊P14
右上段の解答
誤：
$\frac{n(n-3)}{n}$
正：
$\frac{n(n-3)}{2}$

実用数学技能検定　
過去問題集　数学検定4級（2022年4月30日初版発行）

2022年4月30日に発売いたしました「実用数学技能検定　過去問題集　数学検定4級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
本冊P83
問題6（14）
誤：
２けた正の整数と，
正：
２けたの正の整数と，

実用数学技能検定　
過去問題集　算数検定6級（2021年4月30日初版発行）

2021年4月30日に発売いたしました「実用数学技能検定　過去問題集　算数検定6級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
別冊P61
問題11（30）図中の出席番号
誤：
（2個めの下の番号 左から）
①，④，③，⑤，②
（4個めの下の番号 左から）
①，⑤，③，②，④
（5個めの下の番号 左から）
③，④，①，⑤，②
正：
（2個めの下の番号 左から）
①，⑤，③，②，④
（4個めの下の番号 左から）
①，④，③，⑤，②
（5個めの下の番号 左から）
③，⑤，①，②，④
別冊P62
問題11（30）別の解き方
図中の出席番号（上下2つの図共通）
誤：
（1個めの下の番号 左から）
③，⑤，①，②，④
（2個めの下の番号 左から）
①，④，③，⑤，②
正：
（1個めの下の番号 左から）
③，④，①，⑤，②
（2個めの下の番号 左から）
①，⑤，③，②，④

実用数学技能検定　
過去問題集　算数検定10級（2021年4月30日初版発行）

2021年4月30日に発売いたしました「実用数学技能検定　過去問題集　算数検定10級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P63
問題4（16）の図の線の長さ
誤：
短いほうの線の長さが1.1cm程度
正：
短いほうの線の長さが1.5cm

実用数学技能検定　要点整理

実用数学技能検定　
要点整理　数学検定準1級（2024年5月3日初版発行）

2024年5月3日に発売いたしました「実用数学技能検定　要点整理　数学検定準1級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P69
練習問題5 3行め
誤：
$AC=\vec{c}$
正：
$\vec{AC}=\vec{c}$
P88
例3 $z^6$の式と答え
誤：
$z^6 = \sim = 8 \cdot 1 = 8$
正：
$z^6 = \sim = 8 \cdot i = 8i$
P118
基本問題3 ポイント
誤：
$\cos^2\alpha = \displaystyle \frac{1 + \cos\alpha}{2}$
正：
$\cos^2\alpha = \displaystyle \frac{1 + \cos2\alpha}{2}$
P144
応用問題2 下から1行め
誤：
$\displaystyle \frac{1}{6}(n+1)(n+2)$
正：
$\displaystyle \frac{1}{6}n(n+1)(n+2)$
P149
練習問題9(2)、別冊45ページ 練習問題9(2) 8行め
誤：
…$+ 3^3 +$…
正：
…$+ 3^2 +$…
P170
9行目テスト(2) 答え
誤：
$y' = 20x^3(x^2+1)^4$
正：
$y' = 20x^3(x^4+1)^4$
P205
応用問題7(3) 解説の2行め
誤：
$\displaystyle x\int^{2\pi}_{0}(1-\cos t)^2\cdot(1-\cos t)dt$
正：
$\displaystyle \pi\int^{2\pi}_{0}(1-\cos t)^2\cdot(1-\cos t)dt$
P212
「4 二項分布」例1 2行め
誤：
$^5C^1$
正：
$^5C^4$
別冊20ページ
問題9
誤：
$\vec{AK}$
正：
$\vec{AI}$
別冊62ページ
練習問題9(2) 解説の増減表内
誤：
極大 $\dfrac{27}{{\rm e}^e}$
正：
極大 $\dfrac{27}{{\rm e}^3}$
別冊70ページ
練習問題10(2) 解説の9行め
誤：
$\displaystyle V_{2} = \pi\int^{\frac{\pi}{2}}_{\pi}{x_{2}}^{2}dy_{1} - \pi\int^{\frac{\pi}{2}}_{0}{x_{1}}^{2}dy_{1}$
正：
$\displaystyle V_{2} = \pi\int^{1}_{0}{x_{2}}^{2}dy_{1} - \pi\int^{1}_{0}{x_{1}}^{2}dy_{1}$

実用数学技能検定　
要点整理　数学検定準1級（2014年5月12日初版発行）

2014年5月12日に発売いたしました「実用数学技能検定　要点整理　数学検定準1級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P12
「対数関数の導関数」第2式
誤：
$(log_{e}x)'$
正：
$(log_{a}x)'$
P19の1行め
誤：
$k+10$
正：
$(k+10)^2$
P34の4行め
誤：
底が$10$である対数を$log_{10}M$を
正：
底が$10$である対数$log_{10}M$を
P58の1行め
誤：
$| \vec{a} |=5$
正：
$| \vec{a} |=4$
P93
大問1の解き方
誤：
$1^2+4i^2$
$1^2+9i^2$
正：
$1+4$
$1+9$
P95
応用問題5(2)の解き方の2行め
誤：
$r$
正：
$\gamma$
P107
上段の解き方		 3行めの下に一文追加
「$a$，$b$は実数だから，$-11+a+b$，$-2+2a$も実数である。」
P107
上段の答え
誤：
$a=-1$
正：
$a=1$
P131
問題3（1）解き方の2行め
誤：
$\displaystyle S_n=\Bigl(\frac{1}{2}-\frac{1}{3}\Bigr)+\Bigl(\frac{1}{3}+\frac{1}{4}\Bigr)+\cdots+\Bigl(\frac{1}{n+1}-\frac{1}{n+2}\Bigr)$
正：
$\displaystyle S_n=\Bigl(\frac{1}{2}-\frac{1}{3}\Bigr)+\Bigl(\frac{1}{3}-\frac{1}{4}\Bigr)+\cdots+\Bigl(\frac{1}{n+1}-\frac{1}{n+2}\Bigr)$
P131 問題3（1）解き方の2行め
誤：
$\displaystyle S_n=\Bigl(\frac{1}{2}-\frac{1}{3}\Bigr)+\Bigl(\frac{1}{3}+\frac{1}{4}\Bigr)+$
$\displaystyle \cdots+\Bigl(\frac{1}{n+1}-\frac{1}{n+2}\Bigr)$
正：
$\displaystyle S_n=\Bigl(\frac{1}{2}-\frac{1}{3}\Bigr)+\Bigl(\frac{1}{3}-\frac{1}{4}\Bigr)+$
$\displaystyle \cdots+\Bigl(\frac{1}{n+1}-\frac{1}{n+2}\Bigr)$
P143
基本問題2(2) 解説の1行め
誤：
$y$
正：
$y'$
P155の2行め
誤：
ただし，\( \displaystyle \lim_{x \to-∞} \frac{log_{e}x}{x} = 0\) は
正：
ただし，\( \displaystyle \lim_{x \to∞} \frac{log_{e}x}{x} = 0\) は
P180 ポイント
誤：
$p$は正の整数
正：
$n$は正の整数
P180の下から2行め
誤：
$p=3n+2$
正：
$p=3n-1$
P181、P182
応用問題２の解き方と答え
誤：
最大値$-1$
正：
最小値$-1$
別冊P3の解答⑤
誤：
$3^3-2^2$
正：
$3^3-2^3$
別冊P8
右側の下から2行め
誤：
$\frac{y}{3}$
正：
$\frac{y}{5}$
別冊P21
左側の10行め
誤：
$)E$
正：
$\}E$
別冊P23
左側の15行め、16行め
誤：
①より，$ω^5=ω^3・ω^2=ω^2$　②より
正：
$ω^5=ω^3・ω^2=ω^2$　（※）より
別冊P23
右側の下から1行め
誤：
$\dfrac{\sqrt{3+(-\sqrt{3})^2}}{2}$
正：
$\dfrac{\sqrt{3^2+(-\sqrt{3})^2}}{2}$
別冊P27
左側の下から2行め
誤：
少なくとも1つは0であることが
正：
少なくとも1つは1であることが
別冊P27
右側14行め
誤：
$\dfrac{6}{ab}>0$
正：
$\dfrac{36}{ab}>0$
別冊P29
左側の②の解き方		 6行めの下に一文追加
「$a$，$b$は実数だから，$3a+2b-3$，$4a+b+11$も実数である。」
別冊P29
右側の③（3）4行め
誤：
$(4-\gamma)(4-\alpha)(4-\gamma)$
正：
$(4-\gamma)(4-\alpha)(4-\beta)$
別冊P35
左側の6行め		 小問番号（1）を削除
別冊P37
②（3）の答え
誤：
$\dfrac{2}{3(2x-1)\sqrt[3]{2x-1}}$
正：
$-\dfrac{2}{3(2x-1)\sqrt[3]{2x-1}}$
別冊P41
左側の③（2）のグラフ
誤：
（極値をとるときの$x$の値）
$-2\sqrt{2}$ ，$2\sqrt{2}$
正：
（極値をとるときの$x$の値）
$-2\sqrt{3}$ ，$2\sqrt{3}$
別冊P45
左側の3行め
誤：
$dt=\dfrac{3}{{\rm cos}^2θ}dθ$
正：
$dt=\dfrac{\sqrt{3}}{{\rm cos}^2θ}dθ$
別冊P50
左側の10行め
誤：
$\begin{pmatrix}\dfrac{dx}{dy}\end{pmatrix}^2+\begin{pmatrix}\dfrac{dy}{dx}\end{pmatrix}^2$
正：
$\begin{pmatrix}\dfrac{dx}{dt}\end{pmatrix}^2+\begin{pmatrix}\dfrac{dy}{dt}\end{pmatrix}^2$

実用数学技能検定　
要点整理　数学検定2級（2023年5月2日初版発行）

2023年5月2日に発売いたしました「実用数学技能検定　要点整理　数学検定2級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P19
応用問題3 解き方 5～6行め
誤：
$6^2$＜$45$，$47$＞$7^2$ であるから
$6^2$＜$23+2\sqrt{130}$＜＝$7^2$
正：
$6^2$＜$45$，$47$＜$7^2$ であるから
$6^2$＜$23+2\sqrt{130}$＜$7^2$
P24
応用問題 解き方 1行め
誤：
$3y＋7y＝1$…➁
正：
$3y＋7z＝1$…➁

実用数学技能検定　
要点整理　数学検定2級（2014年5月12日初版発行）

2014年5月12日に発売いたしました「実用数学技能検定　要点整理　数学検定2級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P54
基本問題1の解き方
誤：
$\{y-(-4)^2\}$
正：
$\{y-(-4)\}^2$
P135
応用問題2（2）問題と解き方
誤：
$b_n$=$\frac{a_{n+1}}{a_n}$$(n≧2)$
正：
$b_n$=$\frac{a_{n+1}}{a_n}$
誤：
$=3n-1$
正：
$=3n-1$この式は$n=1$のときも成り立つ。

実用数学技能検定　
要点整理　 数学検定準2級（2022年12月28日初版発行）

2014年1月10日に発売いたしました「実用数学技能検定　要点整理　数学検定準2級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P34
問題2（4） 答え
誤：
7
正：
13
P35
問題2（4） 解説4〜6行め
誤：
$13\cdot(13+14)=(20-x)\cdot(20+x)$
$x^2=49$
$x>0$より，$x=7$　答え $7$
正：
$16\cdot(16+19)=(27-x)\cdot(27+x)$
$x^2=169$
$x>0$より，$x=13$　答え $13$
P154
問題2（4）
誤：
正：

実用数学技能検定　
要点整理　 数学検定準2級（2014年1月10日初版発行）

2014年1月10日に発売いたしました「実用数学技能検定　要点整理　数学検定準2級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P46
「練習問題④（1）」
誤：
∠A＝∠C
正：
∠B＝∠C
P77
「練習問題②（3）」
誤：
3より小さくなる
正：
0，1，2のいずれかになる
P112
「基本問題2（1）」別解の図
誤：
（AE＝）4cm
正：
（AE＝）5cm
別冊P37
問題4の解説
誤：
面積比
正：
体積比

実用数学技能検定　
要点整理　 数学検定3級（2021年4月30日初版発行）

2021年4月30日に発売いたしました「実用数学技能検定　要点整理　数学検定3級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P11
円周角の定理の説明
誤：
その弧に対する円周角の半分になる。
正：
その弧に対する中心角の半分になる。
P45
基本問題2（2）の問題文
誤：
$x＋2y＝-13$
正：
$x＋2y＝13$
P118
基本問題1（1）の答え
誤：
AB＝EFならば，△ABC≡△DEFである。
正：
AB＝DEならば，△ABC≡△DEFである。
P165
応用問題　＜解き方＞ア　2行め
誤：
記録が12回以上の人数はもっとも多くて4人であるが
正：
記録が12回以上の人数はもっとも多くて7人であるが
別冊P21
大問3の解説
誤：
A会場: $y=10000$
正：
A会場: $y=100000$
別冊P45 左側
大問1（2）の解説
誤：
B=6で，C=4，またはC=8のいずれかの場合が考えられる。 (中略）A=3のとき，計算結果が最小になるのは，B=3，C=5のときであるが，33×35=1155より，不適。
よって，A=1，2のいずれか，B=3，7，9のときC=5，またはB=6のときC=4，8の計10通りであり，問題に適しているのは，A=2，B=6，C=4である。
正：
B=6で，C=2，4，8のいずれかの場合が考えられる。（中略）A=3のとき，計算結果が最小になるのは，B=6，C=2のときであるが，36×32=1152より，不適。
よって，A=1，2のいずれか，B=3，7，9のときC=5，またはB=6のときC=2，4，8の計12通りであり，問題に適しているのは，A=2，B=6，C=4である。

実用数学技能検定　
要点整理　 数学検定3級（2014年1月10日初版発行）

2014年1月10日に発売いたしました「実用数学技能検定　要点整理　数学検定3級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P31
練習問題⑦（1）
誤：
あゆみさんが自転車で走った時間を$x$分として
正：
あゆみさんが出発してから父に追いつかれるまでの時間を$x$分として

実用数学技能検定　
要点整理　 数学検定4級（2021年4月30日初版発行）

2021年4月30日に発売いたしました「実用数学技能検定　要点整理　数学検定4級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P26
基本問題3（3）の解き方
誤：
累乗を先に計算する
正：
乗法を先に計算する
P144
発展問題 問題1 10行め
誤：
∠BPA＝∠QGF＝90°…イ
正：
∠BPA＝∠FQG＝90°…イ
別冊P28 右側の8行め
問題4の解答
誤：
△AED＝△BFA
正：
△AED≡△BFA
別冊P33
大問4の解説
誤：
イ…最頻値は度数のもっとも大きい54g以上58g未満の階級の階級値だから，56gである。
正：
イ…最頻値は度数のもっとも大きい58g以上62g未満の階級の階級値だから，60gである。

実用数学技能検定　
要点整理　 数学検定5級（2021年4月30日初版発行）

2021年4月30日に発売いたしました「実用数学技能検定　要点整理　数学検定5級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P61
テスト（1）の答え
誤：
時速45m
正：
時速45km
P64
発展問題（2）の解き方
誤：
なおきさんがひろとさんの1周遅れになった
正：
ひろとさんがなおきさんの1周遅れになった
P132
「3 立体の表面積と体積」のチェック！
誤：
立体の体積
角柱・円柱の表面積　…
角錐・円錐の表面積　…
球の表面積　…
正：
立体の体積
角柱・円柱の体積　…
角錐・円錐の体積　…
球の体積　…
別冊P16 右側の6行め
大問3(4)の解答
誤：
$\dfrac{12}{5}$
正：
$\dfrac{24}{5}$
別冊P17 右側の5行め
大問3(4)の解説
誤：
答え$\dfrac{12}{5}$
正：
答え$\dfrac{24}{5}$

実用数学技能検定　
要点整理　算数検定7級（2019年4月25日初版発行）

2019年4月25日に発売いたしました「実用数学技能検定　要点整理　算数検定7級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P19
発展問題1（2）（3）の答え
誤：
（2）10011222333444
（3）44433322211100
正：
（2）100011222333444
（3）444333222110100

実用数学技能検定　
要点整理　算数検定8級（2014年1月10日初版発行）

2014年1月10日に発売いたしました「実用数学技能検定　要点整理　算数検定8級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
別冊解答P25
解答①（1）〜（4）
誤：
（1）ア…７　イ…５　ウ…６
（2）ア…１　イ…７　ウ…６
（3）ア…９　イ…３　ウ…４
（4）ア…８　イ…７　ウ…６
正：
（1）ア…５　イ…６　ウ…７
（2）ア…６　イ…１　ウ…７
（3）ア…４　イ…３　ウ…９
（4）ア…６　イ…８　ウ…７

実用数学技能検定　
要点整理　算数検定9級（2019年4月25日初版発行）

2019年4月25日に発売いたしました「実用数学技能検定　要点整理　算数検定9級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P123
きほんもんだい２（2）のとき方
誤：
1cm
正：
1ｍ
別冊P8
かいとう１（19）
誤：
21070
正：
22540

実用数学技能検定　
要点整理　算数検定10級（2019年4月25日初版発行）

2019年4月25日に発売いたしました「実用数学技能検定　要点整理　算数検定10級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P128
おうようもんだい１（1）の答え
誤：
正：

実用数学技能検定　
要点整理　算数検定11級（2019年4月25日初版発行）

2019年4月25日に発売いたしました「実用数学技能検定　要点整理　算数検定11級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P39
きほんもんだい1（1）の答え
誤：
7
正：
8
P109
きほんもんだい1（2）の答え
誤：
6じ30ぷん
正：
9じ30ぷん

実用数学技能検定　
要点整理　算数検定11級（2014年1月10日初版発行）

2014年1月10日に発売いたしました「実用数学技能検定　要点整理　算数検定11級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P9
正：
11級の検定基準（抄）
※以下のページからもご確認いただけます。

11級の概要・検定の内容

実用数学技能検定　発見

実用数学技能検定　準1級
［完全解説問題集］発見
【第2版】（2015年7月21日初版発行）

2015年7月21日に発売いたしました「実用数学技能検定　準1級［完全解説問題集］発見【第2版】」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P22
問題5の解答・解説 (ii)
誤：
余りが3の倍数
正：
和が3の倍数
P32
問題5①　解答2行め
誤：
$ I=\displaystyle\frac{1}{2}e^{2x}sinxdx-\int\displaystyle\frac{1}{2}e^{2x}cosxdx$
正：
$ I=\displaystyle\frac{1}{2}e^{2x}sinx-\int\displaystyle\frac{1}{2}e^{2x}cosxdx$
P40
問題2の解答・解説
誤：
特別方程式
正：
特性方程式
P43
参考①
誤：
極限値（2.7818……）
正：
極限値（2.7182……）
P46
参考の1行め
誤：
（2）ですべてのマスを～同じことである。
正：
（1）の図に関連する問題として，この図で一筆書きができるかどうかについて考える。
P62
問題2（1）の解答・解説
誤：
$b≠0$ であるので，$ax+by+c=0$を変形して，
（中略）$m=\displaystyle\frac{b}{a}$
よって，直線 $l$ の法線ベクトルの1つは $\vec{n}=(a，b)$
正：
$ab≠0$ のとき，$ax+by+c=0$を変形して，
（中略）$m=\displaystyle\frac{b}{a}$
より，$l$ の法線ベクトルとして$(a，b)$がとれる。 $a＝0$のとき$(0，1)$，$b=0$のとき$(1，0)$がそれぞれ法線ベクトルとなる。
よって，直線 $l$ の法線ベクトルの1つは $\vec{n}=(a，b)$

実用数学技能検定　記述式演習帳

実用数学技能検定　
記述式演習帳　数学検定準1級（2018年4月13日初版発行）

2018年4月13日に発売いたしました「実用数学技能検定　記述式演習帳　数学検定準1級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P30
例題1の2行め
誤：
$a_2=1$
正：
$a_2=5$
P79
練習問題2の（2）の解答・解説
誤：
$| AC |^2$
正：
$| \vec{AC} |^2$
P176
実践問題2の（2）の解答・解説　3,4行め
誤：
$20-10=80$·$10^{kt_{0}}$
これを変形して，$10^{-kt_{0}}=$$\frac{80}{10}$$=8$
正：
$20-10=80$·$10^{-kt_{0}}$
これを変形して，$10^{kt_{0}}=$$\frac{80}{10}$$=8$
P203
実践問題2の（1）の解答・解説　右側9行め
誤：
\( \displaystyle \lim_{h \to+0} g'(x) = \lim_{h \to-0} g'(x) = 0 = g'(0)\)
正：
\( \displaystyle \lim_{x \to+0} g'(x) = \lim_{x \to-0} g'(x) = 0 = g'(0)\)

実用数学技能検定　
記述式演習帳　数学検定2級（2018年3月16日初版発行）

2018年3月16日に発売いたしました「実用数学技能検定　記述式演習帳　数学検定2級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P65
実践問題2の1行め
誤：
次の式を満たす$x$は，何桁の整数ですか。
正：
次の式を満たす$x$の整数部分は何桁ですか。
P147
実践問題2の解答・解説
誤：
よって，$x$は6桁の数である。
正：
よって，$x$の整数部分は6桁である。

実用数学技能検定　文章題入門帳

実用数学技能検定　
文章題入門帳　算数検定11級（2018年3月16日初版発行）

2018年3月16日に発売いたしました「実用数学技能検定　文章題入門帳　算数検定11級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P60 れいだい
誤：
こたえ
正：
こたえ
P86
といてみよう２
誤：
かだんに　チューリップ，ばら，ゆりの　じゅんばんで
正：
かだんに　チューリップ，ゆり，ばらの　じゅんばんで

親子ではじめよう　算数検定

親子ではじめよう　
算数検定6級（2024年5月3日初版発行）

2024年5月3日に発売いたしました「親子ではじめよう　算数検定6級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P119
問題3（1） 上から6行め
誤：
19.15cm
正：
19.15m
P89
練習問題4 3行め
誤：
から までの中から
正：
から までの中から

親子ではじめよう　
算数検定6級（2017年7月20日初版発行）

2017年7月20日に発売いたしました「親子ではじめよう　算数検定6級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P126
算数パーク 解答・解説
誤：
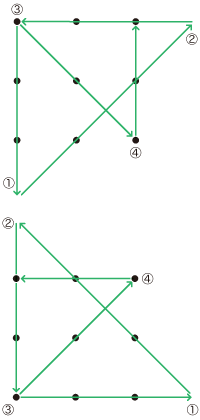
正：

親子ではじめよう　
算数検定7級（2024年5月3日初版発行）

2024年5月3日に発売いたしました「親子ではじめよう　算数検定7級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P65
例題2（2） 1行め
誤：
$18$と$36$の公約数
正：
$18$と$30$の公約数
P72
算数パーク　面積分けパズルの例
誤：
右向き矢印の例は○ 下向き矢印の例は×
正：
右向き矢印の例は× 下向き矢印の例は○

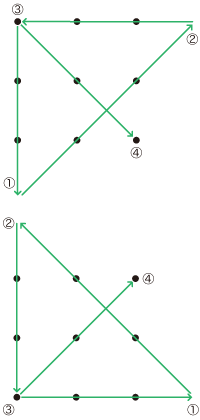
親子ではじめよう　
算数検定7級（2017年7月20日初版発行）

2017年7月20日に発売いたしました「親子ではじめよう　算数検定7級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P71
例題1（1）
誤：
250m, 180m
正：
250円, 180円

親子ではじめよう　
算数検定8級（2024年5月3日初版発行）

2024年5月3日に発売いたしました「親子ではじめよう　算数検定8級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P67
練習問題4 1行め
誤：
一万の位
正：
百の位
P131
問題4（2） 1行め
誤：
弟
正：
お父さん

親子ではじめよう　
算数検定9級（2017年7月20日初版発行）

2017年7月20日に発売いたしました「親子ではじめよう　算数検定9級」におきまして、記載に誤りがありました。
読者のみなさまならびに関係各位にご迷惑をおかけしましたことをお詫びするとともに、ここに訂正させていただきます。

訂正箇所 誤 正
P43
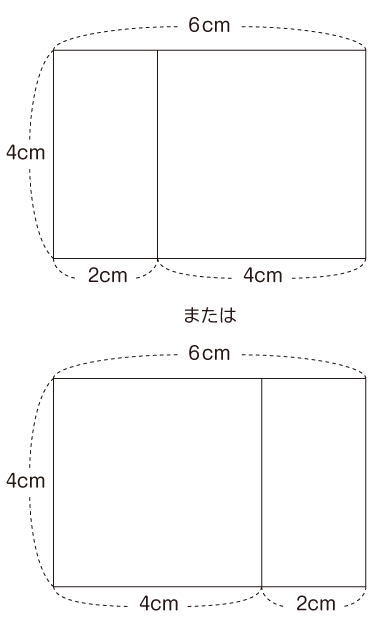
れんしゅうもんだい③
誤：
直線を2本引いて，3つの正方形をつくります。（中略）かきいれましょう。正方形の大きさは，ちがっていてもよいものとします。
正：
直線を1本引いて，長方形と正方形に分けます。（中略）かきいれましょう。
P46
れんしゅうもんだい①
誤：
作 （ はこ ） ります
正：
作 （ つく ） ります
P108
かいとう③
誤：
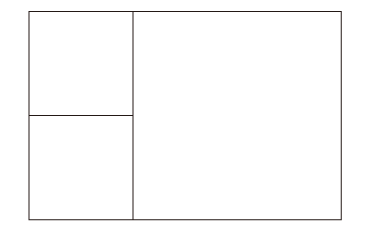
正：
P109
かいせつ③
誤：
1辺の長さが6cmの正方形1つと1辺の長さが3cmの正方形2つに切り分けられます。
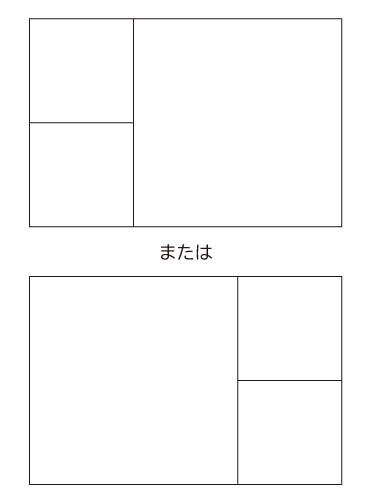
正：
たて4cm，横2cmの長方形と，1辺の長さが4cmの正方形に分けられます。