個人受検の申し込み
検定日一覧
関連書籍
検定過去問題
数学検定で一歩踏み出そう！
検定情報
個人受検にはA日程とB日程があり、検定日や実施階級などが異なります。
個人受検A日程（年3回）
- 年3回全国で開催
- 受検「地域」選択
- 定員なし
実施階級：1～11級（会場による）、かず・かたち実施
-
申込受付終了 第440回 2025年
4月13日日実施
申込受付期間 2月10日月 〜 3月4日火
-
申込受付終了 第444回 2025年
7月27日日実施
申込受付期間 5月26日月 〜 6月17日火
-
申込受付終了 第448回 2025年
10月26日日実施
申込受付期間 8月25日月 〜 9月17日水
ネットはもちろん、
LINEでも申し込み可能
個人受検B日程 直近の日程
- 通年で随時開催
- 受検「会場」選択
- 定員あり
実施階級：準1～11級（検定日、会場による）
-
申込受付中 第452回 2025年
12月6日土実施
申込受付期間 10月6日月 〜 11月5日水
-
申込受付前 第453回 2026年
1月17日土実施
申込受付期間 11月10日月 〜 12月9日火
-
申込受付前 第454回 2026年
2月13日金実施
申込受付期間 12月15日月 〜 1月14日水
まずは近くの検定会場を調べてみよう
入試優遇も！特長とメリット
実用数学技能検定は
文部科学省後援の検定！
高校・大学入試などで
「入試優遇制度」が
活用できます！
高等専門学校・高等学校・中学校
全国990校以上！
※2025年1月現在。当協会調べ
高校入試における生徒の評価基準として、学科試験の成績だけではなく、中学校在学中の実用数学技能検定の取得を活用する学校が多数あります。入試時の点数加算から参考要素とするなど、それぞれの学校において、内容はさまざまです。
下記のリンクから、入試における活用校を検索し、入試優遇措置の実施状況をご確認になれます。
日々の学習に活用して、
数学力をアップしよう！
苦手や弱点がわかる
「個別成績票」が
発行されます！
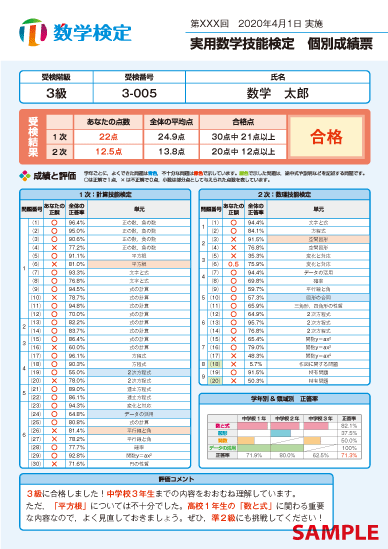
個別成績票表面
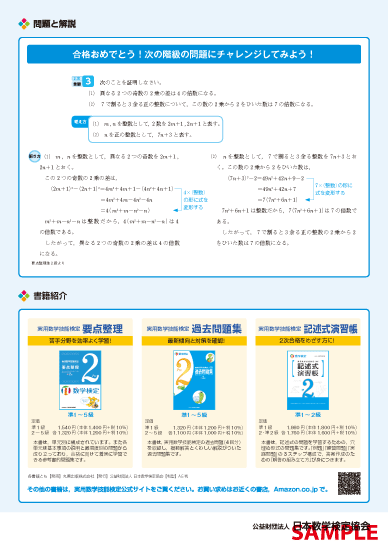
個別成績票裏面
実用数学技能検定（数学検定・算数検定）のすべての受検者の方に、受検後も引き続き算数・数学の学習に励んでいただけるよう、個別成績票を発行しています。
個別成績票には、小問ごとの成績に加え、問題の内容、結果を表すグラフ、評価コメント、成績に応じたチャレンジ問題などを掲載しています。検定結果を合否や正誤だけでとらえるのではなく、出題された内容と照らし合わせて見直すことで、今後の学習に生かすことができます。
思考力・判断力・表現力の向上に！
数学検定はすべて
「記述式」の検定です！
数理技能検定の採点例①
数理技能検定の採点例②
実用数学技能検定（数学検定・算数検定）は、計算結果のみではなく、それにいたる解法の説明や、計算式などを記述します。マークシート方式のように与えられた選択肢のなかから正解を選ぶ解答方式では評価できない理解度についても判定します。正解していなくても、途中までの考え方が正しい場合は、部分点が付与されます。
※実際の検定では、解答用紙は返却されません。
検定過去問題にチャレンジ！
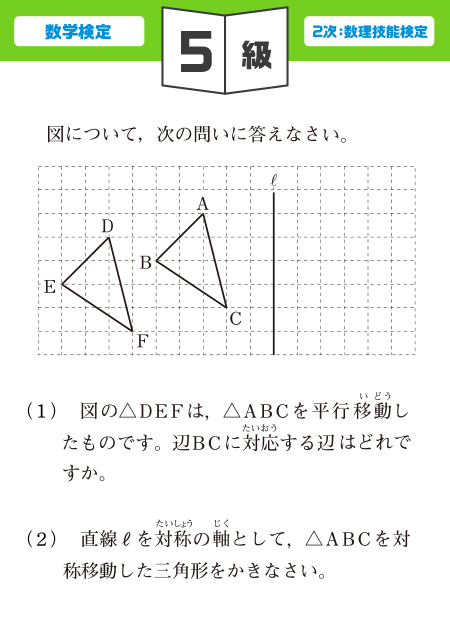
5級の解答を見る
閉じる
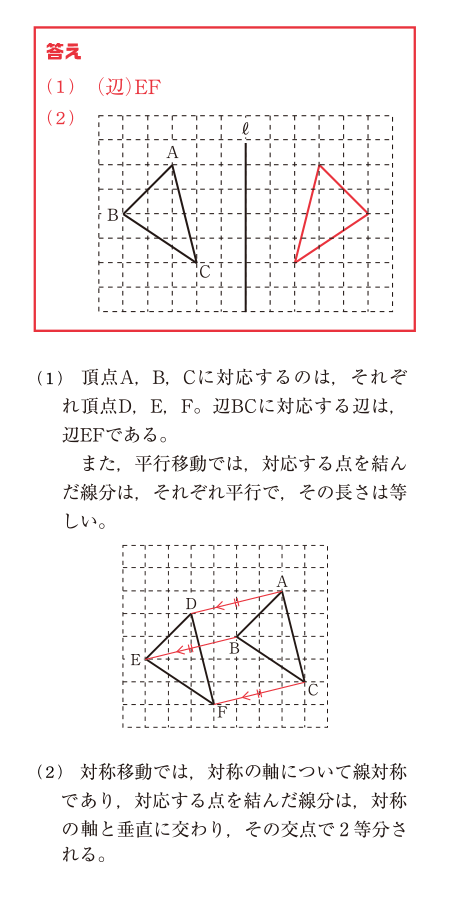
3級の解答を見る
閉じる
お申し込みはこちらから
個人受検にはA日程とB日程があり、検定日や実施階級などが異なります。
個人受検A日程（年3回）
- 年3回全国で開催
- 受検「地域」選択
- 定員なし
実施階級：1～11級（会場による）、かず・かたち実施
-
申込受付終了 第440回 2025年
4月13日日実施
申込受付期間 2月10日月 〜 3月4日火
-
申込受付終了 第444回 2025年
7月27日日実施
申込受付期間 5月26日月 〜 6月17日火
-
申込受付終了 第448回 2025年
10月26日日実施
申込受付期間 8月25日月 〜 9月17日水
ネットはもちろん、
LINEでも申し込み可能
個人受検B日程 直近の日程
- 通年で随時開催
- 受検「会場」選択
- 定員あり
実施階級：準1～11級（検定日、会場による）
-
申込受付中 第452回 2025年
12月6日土実施
申込受付期間 10月6日月 〜 11月5日水
-
申込受付前 第453回 2026年
1月17日土実施
申込受付期間 11月10日月 〜 12月9日火
-
申込受付前 第454回 2026年
2月13日金実施
申込受付期間 12月15日月 〜 1月14日水
まずは近くの検定会場を調べてみよう
調べてみよう目安の階級
中学生の目安となる階級
![5級]()
| 目安の学年 | 中学校1年程度 |
|---|---|
| 構成 | 1次：計算技能検定、2次：数理技能検定があります。 はじめて受検するときは1次・2次両方を受検します。また、1次も2次も同じ日に行います。 |
| 検定料 | 個人受検：4,300円 団体受検：3,800円 |
出題の構成
5級についてくわしく見る
閉じる
![4級]()
| 目安の学年 | 中学校2年程度 |
|---|---|
| 構成 | 1次：計算技能検定、2次：数理技能検定があります。 はじめて受検するときは1次・2次両方を受検します。また、1次も2次も同じ日に行います。 |
| 検定料 | 個人受検：4,300円 団体受検：3,800円 |
出題の構成
4級についてくわしく見る
閉じる
めざせ合格！学習サポート
検定合格に向けた学習や
基礎的な数学力の向上に！
過去問題集や参考書、
「関連書籍」で学習しよう！
過去問題集
要点整理
過去に実際に使われた検定問題を多数収録している「実用数学技能検定 過去問題集」や、単元別に構成された参考書のような問題集で合格に向けて着実に学習できる「実用数学技能検定 要点整理」など、検定合格や基礎的な数学力の向上に向けた学習が行える、さまざまな関連書籍が発行されています。
コンビニプリントで苦手対策！
「単元別プリントドリル」
で苦手を克服しよう！
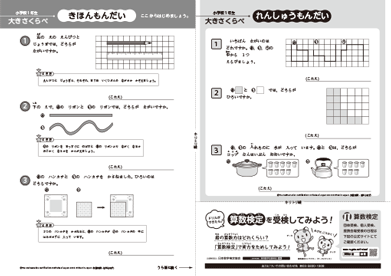
小学生や中学生が苦手意識を持ちやすい単元を取り上げ、「基本問題」「練習問題」「確認テスト」の3段階のステップにまとめました。A3（両面）1枚のプリントドリルです。
お申し込みはこちらから
個人受検にはA日程とB日程があり、検定日や実施階級などが異なります。
個人受検A日程（年3回）
- 年3回全国で開催
- 受検「地域」選択
- 定員なし
実施階級：1～11級（会場による）、かず・かたち実施
-
申込受付終了 第440回 2025年
4月13日日実施
申込受付期間 2月10日月 〜 3月4日火
-
申込受付終了 第444回 2025年
7月27日日実施
申込受付期間 5月26日月 〜 6月17日火
-
申込受付終了 第448回 2025年
10月26日日実施
申込受付期間 8月25日月 〜 9月17日水
ネットはもちろん、
LINEでも申し込み可能
個人受検B日程 直近の日程
- 通年で随時開催
- 受検「会場」選択
- 定員あり
実施階級：準1～11級（検定日、会場による）
-
申込受付中 第452回 2025年
12月6日土実施
申込受付期間 10月6日月 〜 11月5日水
-
申込受付前 第453回 2026年
1月17日土実施
申込受付期間 11月10日月 〜 12月9日火
-
申込受付前 第454回 2026年
2月13日金実施
申込受付期間 12月15日月 〜 1月14日水
まずは近くの検定会場を調べてみよう
学習して良かった！合格体験記
初めての数学検定
5級合格
日野 奏 さん
（神奈川県・中学校1年生）
5級合格
初めての数学検定
日野 奏 さん （神奈川県・中学校1年生）
初めて数学検定に挑戦して、合格できました。すごくうれしいです。
僕が数学検定を受けようと思ったのは、学校からプリントをもらってきて、 両親から受けてみたらと言われたからです。数学は好きなので、試しに受けてみようと思いました。けれど、数学は習いはじめてまだ数か月で、合格できるか不安でした。
母が過去問題をプリントしてくれたので、解いてみました。はじめは「解ける！」と思ったのですが、出題数が多く、問題もかんたんに解けるものばかりではなく、途中でやめてしまいました。受けるのをやめようかとも思いました。
その後、母から小学校5・6年も範囲も入ってるようだと聞き、それなら合格する可能性があるかもと、もう一度解いてみました。まだ習っていない問題は、父に聞いて、解き方がわかりました。ですが、中学校1年の範囲は、過去問題に載っているよりたくさんあるだろうから、わかる問題が出てほしいと願いました。
検定当日は、同じ階級の受検者の人たちは、自分より年上の人ばかりがいるように見えて、緊張しました。見直す時間もないくらいでしたが、全力を出せたと思います。
結果は合格で、とてもうれしかったです。合格証が届いて実感がわいたのと、小学校5・6年の問題はパーフェクトで、中学校1年の問題も半分以上できていて、やった！と思いました。両親も「すごい」とほめてくれました。解けなかった問題は、この学年が終わるまでに解けるようになろうと思います。そして、次の級にも挑戦したいです。
大好きな数学の落とし穴
準2級合格
宇井 星日 さん
（愛知県・中学校3年生）
準2級合格
大好きな数学の落とし穴
宇井 星日 さん （愛知県・中学校3年生）
数検を初めて受検したのは、中学校2年生の夏。とても暑い日で、試験場に行くだけで疲れたのを覚えています。学年相応の3級ということもあり、すんなり合格。結果を見て安堵したのを思い出します。
そして3級に合格し、準2級にも挑戦。テキストを買ってもらい、勉強を開始するのですが、やはり高校数学となると今まで以上に理解する力が求められます。とはいえ、数学は好きでもあり、得意でもあります。
そして迎えた検定当日、団体受検の会場で受検。なんと、1次は満点で合格できると思いました。1次は満点合格したものの、2次はというと、問題を開くと目に入ってきたものが…。
それまで、私は計算問題を正確に解くことを重視して勉強してきました。そのため、2次で出題されるような、思考力を試す問題には不慣れだったのです。
焦りもあり、2次は不合格に終わりました。
一念発起し、再受検を決意。学校の長期休みを利用し、記述力を徹底的に身につけました。そのころ、他の資格試験の勉強をしていたこともあり、一時期は体力的にもたいへんでした。
猛勉強のかいもあり、10点中9.8点で合格。あと0.2点が悔しいところですが、予想を大きく上回る点数で合格できて、本当にうれしく思います。
大好きな教科での勉強にも、落とし穴がありました。2級を受ける際は、落とし穴をきちんと固めてから、検定に臨みたいと思います。
