就職活動に求められる能力はさまざま。その1つが「数学力」です。“ホントに?”と思う人もいるかもしれませんが、実際に就活では、筆記試験など数学力が試される場面もしばしば。また、数学を学ぶことで培われる能力もあるのです。「数学検定(=数検)」は、自身の数学力を証明するもの。これを就活に活用する方法を紹介します!
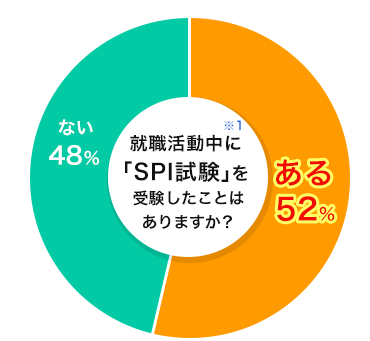
採用選考の関門「SPI」は2人に1人が受験している
就職活動の選考過程で、SPIを受験する就活生は半数以上。もちろん、そこでは数学力が必要な出題があります。また別の調査※2では、「就活を始めて、もっと早く取り組めばよかったこと・時間をかけて取り組みたかったこと」の第3位に、筆記試験(SPI等)対策がランクイン。このように、就活において筆記試験対策は重要な要素だと言えるのです。
就活生って実は……
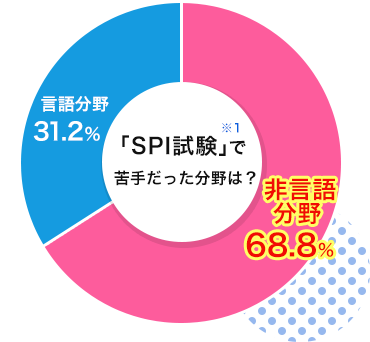
非言語分野が苦手
SPI試験には、非言語/言語の2つの分野があります。調査によれば、数学が含まれる非言語分野が苦手という就活生が約70%。SPI試験に限らず、筆記試験では非言語分野の出題が想定されるので、ここを得意分野にすることが、ほかの就活生との差を生み出すことにつながります。
- ※1 就職活動に関するアンケート/2016年12月/対象:2017年卒 就活内定者及び、社会人歴1~3年め 男女/有効回答数:400件/マイナビ 学生の窓口調べ
- ※2 2017年卒 学生就職モニター調査/2016年8月/対象:2017年卒業予定の全国大学4年生及び院2年生/有効回答数:1,077/新卒採用サポネット調べ
- SPI試験の出題範囲と数検 -
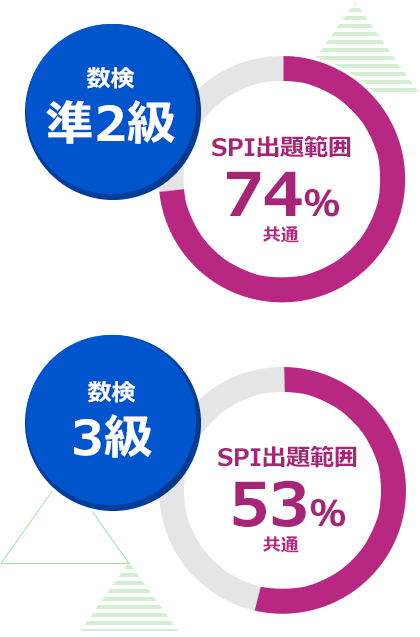
数検はSPI試験対策につながる!
多くの就活生が苦手とするSPI試験の非言語分野。その対策に有効なのが「数検」です。実は、SPI試験の出題範囲は数検の準2級で74%、3級で53%共通しています(年度によって若干異なります)。数検のための勉強が、そのままSPI対策につながるのです。また、数検は自身の能力の証明にもなるので、エントリーシートや履歴書の資格欄にも記載することができます。

- 出題①【数検3級 割合】
-
ゆうきさんはチーズを、60人の子どもに2個ずつ配るために、全部で120個以上用意します。A、B、Cの3つの店のどこか1つの店でチーズを買います。チーズは1箱20個入りのものと1箱50個入りのものがあります。それぞれの店で扱っている商品とその1箱の値段は、表のとおりです。このとき、次の問いに答えなさい。ただし、消費税は値段に含まれているので、考える必要はありません。
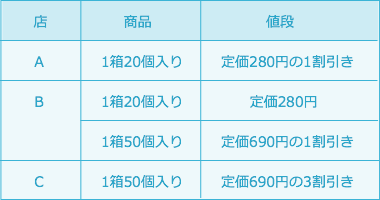
- 問題
- どの店で買うと、いちばん安く用意できますか。A、B、Cの中から1つ選んで、答えなさい。また、そのときの代金も答えなさい。<正答達成率:62.7%>
- 解答
- 店:C 代金:1449円
- [解説]
- 店Aのチーズ1箱の値段は、
280×(1-0.1)=252(円)
これを6箱買うと
252×6=1512(円)…① - 店Bの20個入りのチーズ1箱の値段は280円なので、これを6個買うと
280×6=1680(円)…② - 店Bの50個入りのチーズ1箱の値段は
690×(1-0.1)=621(円) - チーズは120個以上必要なので、3箱買うと
621×3=1863(円)…③ - 50個入りを2箱、20個入りを1箱買うと
621×2+280=1522(円)…④ - 店Cのチーズ1箱の値段は、
690×(1-0.3)=483(円) - これを3箱買うと、
483×3=1449(円)…⑤ - ①~⑤の中でいちばん安いのは⑤なので、答えは店Cで、値段は1449円である。
- 出題②【数検準2級 場合の数】
-
男子8人、女子7人の計15人の中から、6人の委員を選ぶとき、次の問いに答えなさい。
- 問題1
- 6人とも男子となるような選び方は全部で何通りありますか。この問題は答えだけを書いてください。<正答達成率:62.9%>
- 解答
- 28通り
- [解説]
- 6人とも男子となる選び方は、男子8人の中から6人の委員を選ぶときの場合の数だけあるので
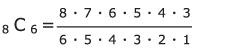
=28(通り)
- 問題2
- 男子と女子がどちらも含まれるような選び方は全部で何通りありますか。<正答達成率:45.7%>
- 解答
- 4970通り
- [解説]
- 委員の選び方の総数は
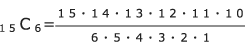
=5005(通り) - このうち、6人とも男子となる選び方は、問題1より28通りである。
6人とも女子となる選び方は
7C6=7(通り)
よって、求める場合の数は
5005−(28+7)=4970(通り)

数学検定2級保有野口さん(大学3年生)
数検に挑戦し苦手意識を克服。
ES・面接で数検所持をアピール
高校3年の6月に数検2級を取得しました。数学は苦手科目でしたが、資格を取るという目標をモチベーションにして必死に勉強。その結果合格したことで、苦手意識の克服にもなりました。
大学では植物や農作物の研究をしています。理数系の要素も多く出てくるので数学力は必要です。将来は大学で学んだ生物の知識を生かせる職種に就きたいと考えています。就活中は筆記試験の他にも、エントリーシートや面接で保有資格を聞かれることがあるので、数検もアピール材料にしています。
就活で実感した論理的思考と
数学力の関係

インターンシップの選考過程でグループワークに参加したことがあります。議論や主張を聞いていて「説得力がある」と相手に思わせるには、論理的な思考が大切だと改めて実感しました。最近は大学でも数学系の授業を積極的に受講しています。数学を学ぶことで、論理的な考え方を身につけ、本格化する就活に役立てたいと思います。


就活をしていて大変なのは、志望動機の記入です。文章力が大切なように感じますが、自分の気持ちを簡潔にまとめるには、数学で養える論理的な考え方も必要です。

数学検定3級保有加藤さん(社会人1年目・公務員)
数学好きが高じて数検に挑戦。
満点を取り大きな自信に
もともと数学が好きだったのに加え、当時通っていた学習塾の薦めもあり、中学2年の終わりに数検3級を受けました。検定に向けた勉強はとくにしませんでしたが、学校での授業と日々の勉強の応用で満点を取ることができました。中学生で数検を取得できたことは、当時大きな自信になりましたね。その後も数学の勉強を続け、大学は理系の学部に進みました。
就職活動においても数学力は重要だと感じます。公務員試験には理数系の問題が出ることが多く、私が受けた時は出題の約4割が数学でした。公務員は市民へ説明する仕事が多いので、理数系の論理的な思考力も求められるのだと思います。
就活で役立った数学力。
社会生活では伝達力の礎に

社会に出ると、学生の時とはまた違った形で数学力が必要だと感じます。学生時代は目の前の問題を解くことが第一にあり、その積み重ねで論理的な考え方を養うことができました。一方、社会人になるとより実践的な要素として論理的思考力や伝達力が問われる場面が増えます。私自身、日々の仕事でできるだけわかりやすく話しをすることを心がけています。相手に話を明確に伝えるには、物事をきちんと系統立てて考えることが大切。こうした思考法を養える数学の重要性を改めて実感しているところです。


就活で一番苦労したのは面接。限られた時間で思いを伝えるには、論理的思考力が必要です。それを養う近道が、数学を学ぶことだと思います。

実際に過去の数学検定で出題された問題を公開しています。1級~5級は、検定1回分(1次・2次)の検定問題・解答用紙・模範解答。6級~11級は、検定1回分の検定問題・解答用紙・模範解答を、それぞれご覧になれます。
■2022年検定日(個人受検)
| 検定日 | 申込期間 | 実施階級 | 時間 |
|---|---|---|---|
| 2023年4月16日(日) | 2/13~3/7 | 1~8級、かず・かたち検定 | 午後1~2時(受検証に記載) |
| 2023年7月23日(日) | 5/22~6/13 | 1~8級、かず・かたち検定 | 午後1~2時(受検証に記載) |
| 2023年10月29日(日) | 8/28~9/19 | 1~8級、かず・かたち検定 | 午後1~2時(受検証に記載) |








