数学を探しに行こう!
建設のプロに聞いてみた!
複雑な地形ってどうやって測っているの?
算数・数学ライブラリ「数学を探しに行こう!」では、日常生活や現代社会のなかで算数・数学がどこにひそんでいるのか、役立っているのかをご紹介するコラムです。中学校や高校で学習する数学の単元を中心にしたコラムですので、みなさんの学習との結びつきを感じてみてください!
■建設現場で見た不思議な光景
みなさん、お元気ですか?
突然ですが、実は私、建設現場が大好きなんです。何かが少しずつ作り上げられるところって、おもしろくないですか。

今日も建設現場のそばを通りかかったので、邪魔にならないように、しばし遠くから見学してしまいました。
すると、不思議な光景を見たのです。2人の作業員が現れて、何やら長い巻き尺のようなものを使い始めました。
何をやっているのだろう?
しばらく観察していると、1つ分かりました。どうやら2人は、広い敷地に大きな三角形を作るようにして、三角形の辺の長さを測量していました。辺の長さを測ってはつぎの三角形を作り、巻き尺を伸ばしていました。
いったい、何のために測っているんだろう?疑問がわいたとき、2人の作業が終わって、1人が「よし、これで事務所に戻って計算するぞ!」と言いました。
えぇー、計算!
いったいこれから何の計算をするのでしょうか。とてもとても気になりましたが、2人は移動してしまい、いなくなってしまいました。
■測っていたのは三角形の辺の長さのみ
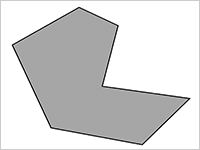
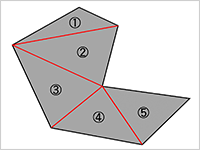
家に帰ってから、振り返ってみました。
巻き尺で測っていた土地は、こんな変な形でした(図1)。これを三角形で分割するように長さを測っていたのです(図2)。
う~ん、何をしていたんだろう? ……もしや、土地の面積を求めるためだったのか。そうだ、きっとそうだ、そうに違いない。
でも、ちょっとおかしい。作業員の方たちは、三角形の3辺の長さのみを測っていました。角度や垂線、「底辺×高さ÷2」の「高さ」を調べているようには見えませんでした。
これだけで三角形の面積は測れるのでしょうか。
■やっぱり敷地の面積を測っていた!
建設現場でどんな計算をしようとしていたのか?気になって仕方がないので、思い切って建設会社の方に尋ねてみました。
教えてくれたのは、ダムや道路、鉄道工事まで、さまざまな建築物を作っていらっしゃる株式会社熊谷組の社員、栃木勇さんです。

「あの測量はですね、舗装する敷地の面積を求めるためにやっていたんですよ」とのこと。
でも、三角形の辺の長さを測っていませんでした?
「複雑な形をした土地でも、折れ点(図形の頂点)を結べば三角形の集まりに分割できますよね。三角形の3つの辺の長さを測れば、面積はかんたんな計算で出せます。そうやって、すべての三角形の面積を足し合わせれば、敷地全体の面積を求められますよね」。
やっぱり、敷地の面積を求めていたのか!ただ、三角形の辺の長さを測るだけで面積が求められるの?
「ヘロンの公式を使えばいいんです」。
■ヘロンの公式が使われていた
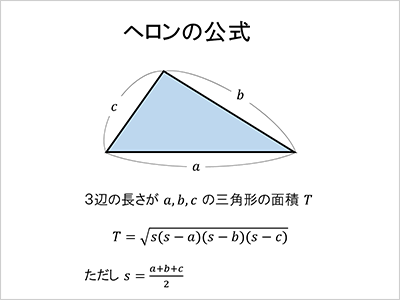
三角形から生まれる美しい数のリズム「三角比」。このリズムから導き出されるとっても便利な公式。
それがヘロンの公式です。なんと、3つの辺の長ささえ分かれば、面積が分かるのです。「高さ」を測る必要もない、角度を調べる必要もない。
長さを測るものさしが1つあれば、三角形の面積をサクッと求められるのです(図3)。
たとえば、三角形の3つの辺が5mと3mと4mなら、
$s=(5+3+4)÷2=6$
$T=\sqrt[]{6(6-5)(6-3)(6-4)}=\sqrt[]{6×1×3×2}=\sqrt[]{36}=6$
この三角形の面積は6m2となります。
高校で学ぶ数学の公式が、実は建設現場でしっかり使われていました! 久々の感動です。
■建設現場ではたくさんの計算が行われていた
建設現場では学校で習った式をよく使うそうです。
「たとえば、地下の施設を作るために掘り出す土の量がどれくらいなのか、あるいは壁の設置に必要な生コンクリートの量はどれくらいなのか、建設現場ではいろいろな数量を正しく知る必要がつぎつぎに出てきます。その数量がきちんとわからないと、材料を注文したり、作業に必要な人や機械の数を決めるときに、無駄が出たり、逆に足りなくなって作業が終わらなかったりしてしまいます。」
その計算は、素人の私たちが想像するより、細かく計算するようです。
たとえば、鉄筋が多く入った構造物の生コンクリートの量を計算するときは、その中に埋まる鉄筋の体積も計算して、壁全体の体積から差し引くとのこと。そうしないと、コンクリートがたくさん余ってしまうことになるそうです。
「生コンクリートは、打ちこむとどんどん固まっていきます。打継ぎ制限時間内に生コンクリートを打設し、一気に作業を終えなくてはなりません。なるべく後から継ぎ足さなくてすむように、きちんと計算して、来てもらうミキサー車の台数を正確に決めます。多めに注文してもいいのですが、生コンクリートがたくさん余ってしまうと無駄が多く出て大きな損失になりますからね。」

ほんの少しだけ余るように数量をはじき出すのが、栃木さんたちの腕の見せどころです。
「たとえば3 mを超すような高い壁を作るとなると、打ちこむ生コンクリートの量も大量で、下の方には多くの荷重がかかるんです。木の板で作った枠(型枠)をしっかり押さえておかないと、壊れてしまい、大事故につながってしまいます。コンクリートの量だけでなく、型枠の強度についての計算も慎重にやるんですよ。」
建設現場では、実にたくさんの計算が行われていたのでした。
■三角比で測りにくいところを測る
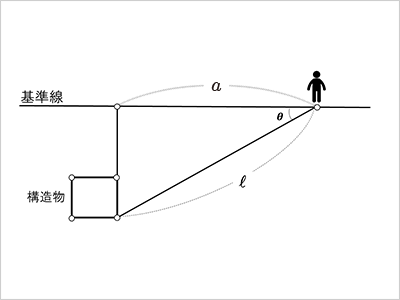
高校で習う三角比が、建設現場ではよく用いられるそうです。
「とくに距離や高さ、角度を調べるときですね。たとえば、新たな構造物を作るときに、その場所を現場で正確に定める必要があります。そのときに三角比が使えるんです(図4)。基準線という、工事の前に機器を使って正確に測っておいた1本の線があれば、かんたんに基準線からの角度と距離が分かります。」
図4のℓを求める場合、まず、基準線の上に立つ自分の場所と、構造物から基準線に引いた垂線と交わる点までの長さを測ります(図では$a$)。
つぎに、自分と建物を結ぶ線と基準線に挟まれた角度θを調べます。これが分かれば、三角比を使って求められるはず!
θが30°で、$a$が40 mの場合
∠30°を作る2辺の関係<比>は、
斜辺が2のときは底辺$\sqrt[]{3}$となる$(cos30°=\frac{\sqrt[]{3}}{2}) $ので、
$\frac{\sqrt[]{3}}{2}=\frac{40}{ℓ}$
ℓ$=\frac{80}{\sqrt[]{3}}=\frac{80\sqrt[]{3}}{3}$ 約46.2m
基準線と角度さえ測ることができれば、どんな長さでも計算で求められるのです!
途中で大きくて底が見えない穴があっても、資材が見えないところまで一面に広げられていても、作りたい構造物がとても高いところだとしても、三角比はどんな空間をも超えて正しい長さを教えてくれます。
実際に建設現場でよく使われていました。
■人の命を守る計算もある
測量と計算が繰り返される建設現場。栃木さんも、これまでたくさんの計算をしてきたそうです。
そんな栃木さんにとって、一番思い出深い計算って何でしょう?尋ねてみました。
「そうですね。入社してすぐに携わったダムの建設現場での計算でしょうか。ダムの天端にゲート操作室とそれを受ける柱を構築する工事での支保工の計算です。ゲート操作室も柱も、どちらも垂直に切り立つダムの上流面に張り出したものです。支保工は、その2つの構造物を作るための、型枠や鉄筋、コンクリート、足場の重さをすべて受ける、受け台(仮設構造物)です。その支保工の上で作業員は作業を行わなくてはなりません。その設計を私が担当することになりました。所長からの指示は、『十分に安全で、とにかく安く作れ』というものでした。」
設置する場所はダムの上流面です。
だから、もし崩れてしまったら、そこで働く人たちはそのまま50 m真下の河床部まで落ちてしまう状況だったとのこと。
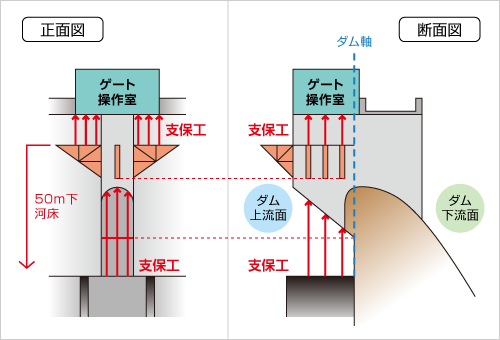
「しかし、必要以上に丈夫過ぎるものを作ってしまっては、逆に撤去が大変になったり、費用がたくさんかかったりしてしまいます。でも、安全は何よりも優先されます。」
栃木さんは、構造物の図面を引いては、想定される大きな力がどこにどれくらい集中するかを計算で求め、それを分散させるには支柱などの部材をどのように入れればよいのか、これも計算していったとのこと。

「人の命に関わる大事故につながりますから、材料断面のたわみの計算や、構造物にかかる荷重の計算は、何度も何度も計算をやり直しました。ようやく設計図ができあがり、支保工を設置して、いよいよ実際に人が乗って作業することになったのですが、今度は、『本当に大丈夫なのか』と気が気ではなくなりました。だから、それから毎朝、必ず現場が見えるところに行って『今日もちゃんとあるな』と確認をしてホッと胸をなでおろすのが日課でした。」
建設現場では、計算が人の命を支えていたなんて、知りませんでした!
今度、建設現場のそばを通ったら、中を少しのぞいてみてください。もしかしたら、現場の監督さんが電卓を片手に計算している光景が見られるかもしれませんよ。
「建築物の設計をするときは、構造計算など難しい計算をするのですが、建設の工事現場では、それほど難しい計算はしません。だから、特別な計算能力は必要ありません。たし算、ひき算、かけ算、わり算の四則計算が基本です。しかし、バタバタする現場の忙しさのなかでも、きちんと間違わないように計算することが何よりも大事になってきます。測量の計算、積算など、正確な数量を計算しなくてはなりません。そのためには、図面をよく見て、さらに現場でもきちんと測って計算し、さらにチェックを何回もしていく。よく若いときは、先輩から『計算は何回もチェックしろ』と言われました。」
特別な能力はいらないけれど、地道に計算して愚直に確かめる。その繰り返しが大事だと、栃木さんは何度も話します。
きっと、建設現場で働く若い人は、計算しながら一人前に成長していくんですね。
みなさんも、数学のテストで計算するときは、こんな栃木さんたちのように、計算ミスがないようにチェックをしたいものですね!
(取材・文/サイエンスライター 宇津木聡史)


今回お話を伺ったのは…

株式会社 熊谷組
副所長 栃木勇さん
(土木事業部 土木部)



