ピラミッド型の体積を求めるとき、なぜ$\displaystyle \frac{1}{3}$をかけるのか?
当協会から小学校6年生向けに配布しているパンフレット「小学校6年生のみなさんへ」にある「ピラミッド型の体積を求められるのは算数のおかげ!」について、くわしく解説します。
ピラミッド型の不思議
パンフレットの内容は、次のようになっています。
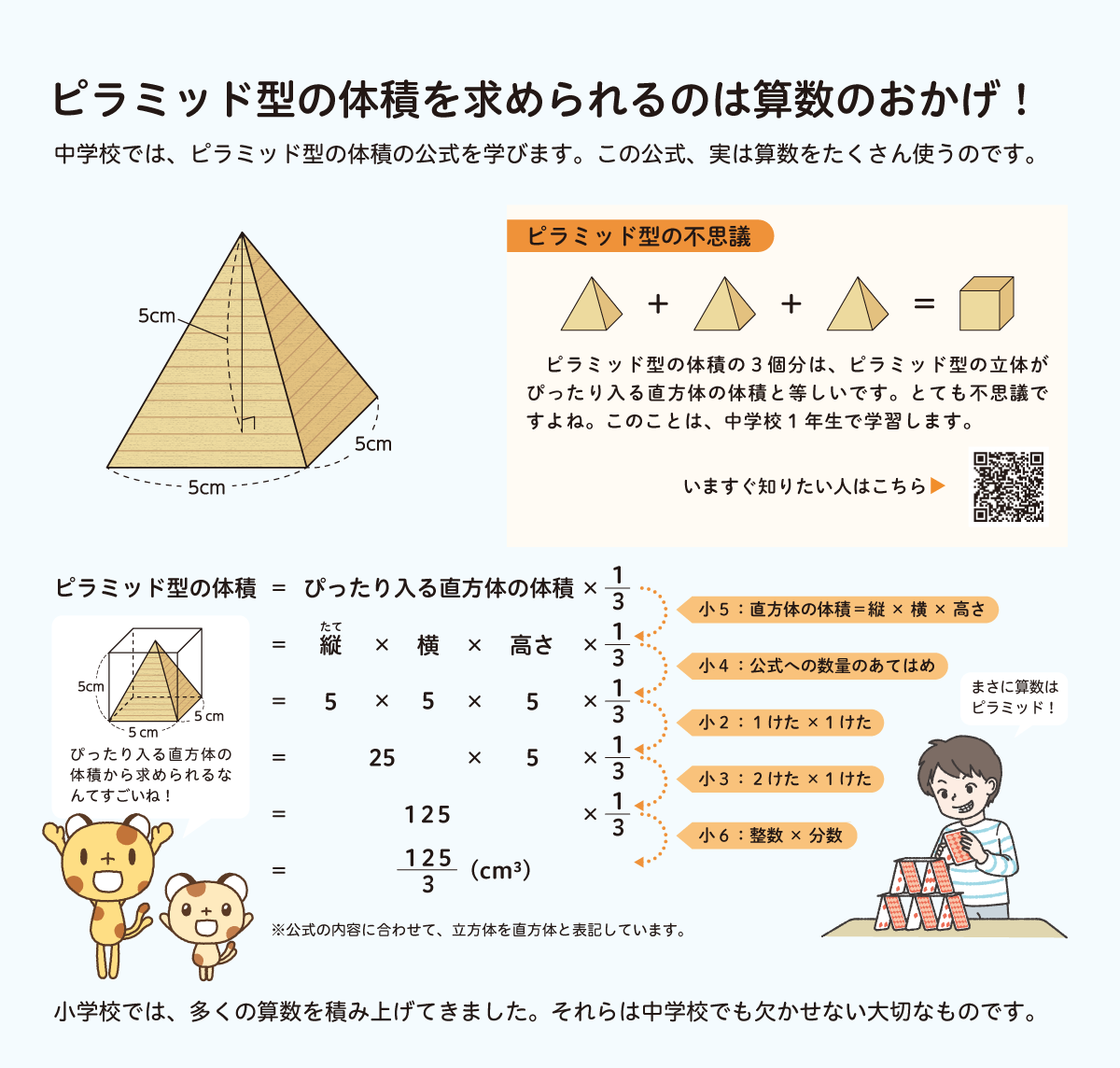
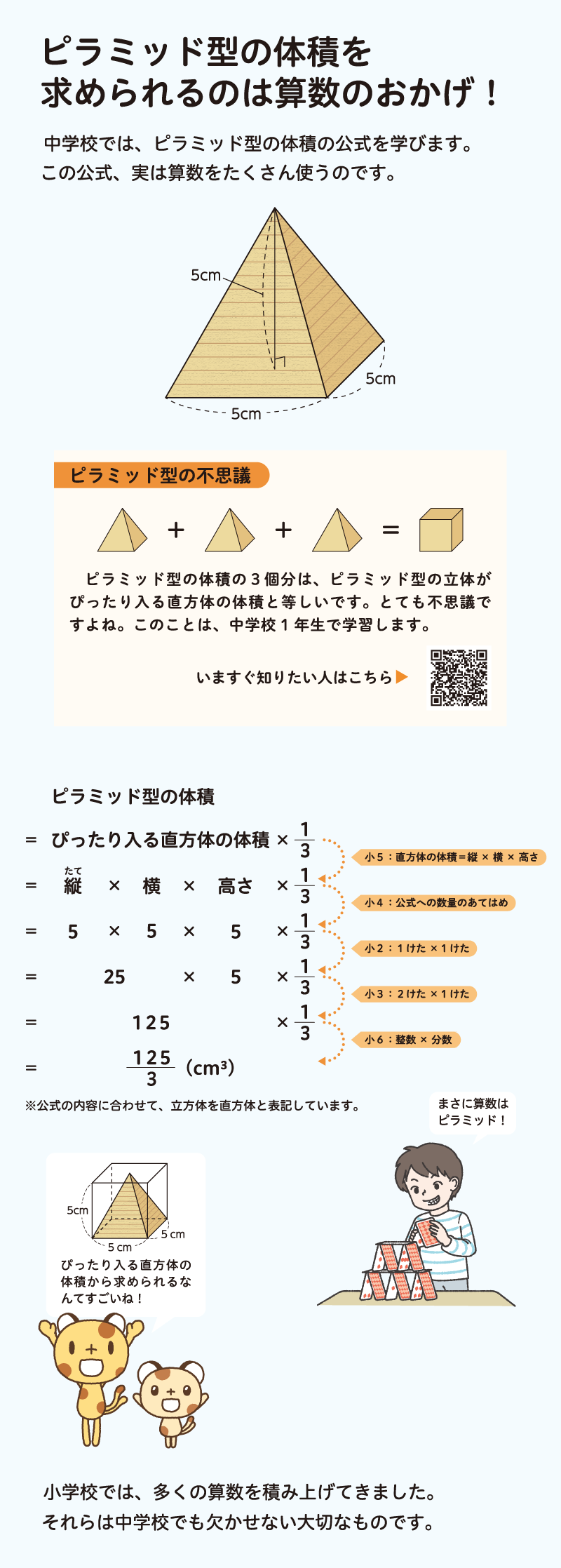
上の「ピラミッド型の不思議」に注目してください。ここに書いてあるように、ピラミッド型の体積の3個分は、ピラミッド型がぴったり入る直方体の体積と等しいことが知られています。このことについて、直方体の辺の長さがすべて等しい場合、すなわち立方体である場合にしぼって考えていきます。
立方体を分割してみよう!
パンフレットに登場しているピラミッド型は縦5cm、横5cm、高さ5cmなので、このピラミッド型がぴったり入る直方体は、1辺が5cmの立方体となります。
この立方体1個とピラミッド型3個が同じ体積だなんて、本当なのでしょうか。こういうときは目で見えるものがわかりやすいです。
上の動画では、立方体を3個の立体に分割しています。分かれた3個の立体をよく見てみてください。すべて同じ大きさで同じ形になっているんです。向きはちがいますが、3個とも、底面が合同な正方形で、形がとがっていて、高さが立方体の1辺と等しいです。大きさも形も同じということは、この3個の立体は体積が等しいということです。立方体を、体積が等しい3個の立体に分けることができました。
この立体、ピラミッド型のようにも見えますが、とがっている部分が正方形の真上にないので、かたむいたピラミッドのような形になっていますね。これはピラミッド型なのでしょうか。
体積を変えずに立体を変形してみよう!
先ほどの分割でできた立体がピラミッド型と同じ体積だといえるなら、ピラミッド型3個と立方体1個が同じ体積だといえそうですよね。これを示すための、とっておきの方法があります。実は、立体は、体積を変えずに変形することができるのです。次の写真を見ながら想像してみてください。

上の写真はイメージですが、立体は、うすーく切ってずらしても体積は変わりません。はがきやトランプなどで同じように変形してみると、実感がわくかもしれませんね。
では、いよいよ、立方体を分割してできた立体を変形してみましょう。次の動画を見てください。
上の動画の変形で、体積は変わっていません。つまり、同じ体積のまま、パンフレットにあるピラミッド型に変形することができました。最後に、わかったことをまとめていきましょう。
分割して変形したら、1個の立方体が3個のピラミッド型になった!
1つめの動画では立方体を3個の立体に分割し、2つめの動画では分割した立体をピラミッド型に変形しましたね。すなわち、1個の立方体が3個のピラミッド型になったということです。このとき、ピラミッド型の体積はすべて等しく、全体の体積に変化はありません。このことから、「縦、横、高さが等しいピラミッド型の体積の3個分は、ピラミッド型がぴったり入る立方体の体積と等しい」ことがわかります。中学校では、このことを用いて、ピラミッド型の体積を求める公式を学びます。
このようにいろいろな算数を積み重ねることで、新しくわかることが増えていきます。中学校の数学が楽しみになってきませんか。ぜひ、これからもいろいろなことに興味をもって、算数・数学の学習を進めてください。



