デジブ用英語

- ページ: 1
- 3rd Kyu & 4th Kyu
�
- ▲TOP

- ページ: 2
- This book contains the following:
Section 1 Problems (Calculation Test) 8 Section 2 Problems (Application Test) 22
1. 2. 3. 4. 5. 6. 7. Warm-up 22 Geometry 25 Equations & Functions 29 Congruent triangles 33 Statistics 35 Geometric constructions 39 Take your time! (puzzles) 42
Answers to Section 1 45 Answers to Section 2 52 Step-by-step solutions to Section 2 57 Appendix: Basic geometric constructions Suken past papers 158
4th Kyu Problems & Answer sheets Set 1 158 4th Kyu Problems & Answer sheets Set 2 171 3rd Kyu Problems & Answer sheets Set 1 184 3rd Kyu Problems & Answer sheets Set 2 197 4th Kyu Answers Set 1 210 4th Kyu Answers Set 2 215 3rd Kyu Answers Set 1 220 3rd Kyu Answers Set 2 225 All problems were taken from past Suken test papers.
144
The Section 2 Problems (Application Test) are divided into seven parts, each of which gives one the opportunity to evaluate one’s strength and weakness. Step-by-step solutions to the problems in Section 2 occupy the biggest portion of the book, and are perhaps the most important. Thus, I have tried to make these solutions clear and detailed by adding the key concepts, alternative solutions, diagrams, and so on. Alternative solutions show how the same problem can be solved in different ways. Also, since visualizing problems is likely to be helpful in solving problems, diagrams are also presented. The last part of the Section 2 (Take your time!) consists of mathematical puzzles. You might be unfamiliar with these problems. But try to spend some time and effort to solve these problems even if you do not know any routine method to solve them. The appendix discusses seven basic geometric constructions. There are 2 sets of Suken past papers at the end of this book. These practices will provide an opportunity to try out under test conditions.
�
- ▲TOP

- ページ: 3
- ➋ Expansion 3rd Kyu
Expand the following expressions.
(1)
(x ¡ 2)(x + 5)
(2)
(x ¡ 2y )(x ¡ 3y )
(3)
(x + m)(y ¡ n)
(4)
(x + 5y )2 + x(x ¡ 10y )
(5)
(2x + 3y )(2x ¡ 3y )
(6)
(x ¡ y + 2)(x ¡ y ¡ 2)
➌ Factoring 3rd Kyu
Factor the following expressions.
(1)
2m ¡ xm + ym
(2)
x2 + 6x + 9
(3)
x2 ¡ 3x ¡ 28
(4)
2x2 ¡ 8x + 8
(5)
(x ¡ y )2 + 8(x ¡ y ) + 16
(6)
(x + 3)2 ¡ 25
�
- ▲TOP

- ページ: 4
- ➋ Geometry 4th Kyu
1
Let the line l be the axis of symmetry for the figure shown on the right. (1) (2) (3) Find the vertex that is symmetric to vertex B with respect to the line l. Find the side that is symmetric to side DE with respect to the line l. What is the total number of axis of symmetry?
2
In the diagram, a circle is inscribed in a square with sides of
4a cm . Include units in your answer. Use ¼ to denote pi.
(1) (2) (3)
What is the area of the square in cm2? What is the area of the circle in cm2? What is the area of the shaded region in cm2?
3
Right-angled triangle ABC is shown on the right. A solid is created by rotating the triangle around the straight line l. (1) (2) Draw a sketch of the solid figure. What is the shape of the cross section when this solid is cut vertically through its axis of rotation? Answer using the most appropriate name. (3) Express the volume of the solid in terms of ¼ .
�
- ▲TOP

- ページ: 5
- 5 (1) Since ABCD is a square, \EAB = 90±.
In 4ABE,
25± + 90± + \AEB = 180± ) \AEB = 65±
4A0 BE is obtained by folding 4ABE
The sum of the degree measures of the interior angles of a triangle is
180±.
along BE, we have
\AEB = \A0 EB = 65±
) \DEA0 = 180± ¡ (65± + 65± ) = 50±
(2) Since BA = BA0 , 4ABA0 is an isosceles triangle.
6 (1) The Pythagorean theorem gives us
(BC) = (AB) + (AC) (BC)2 = 62 + 42 (BC)2 = 52 p BC = § 52
2 2 2
Pythagorean theorem
Since BC > 0, p BC = 52 p = 2 13 p ) BC = 2 13 cm (2) Since \BAC = So, the radius is
1 £ (BC) 2 p ) 13 cm
Three sides of a right-angled triangle relate:
90±
and the triangle is inscribed in a circle, then side
c2 = a2 + b2
BC becomes the diameter of the circle.
What’s the point?
If point B and point C are opposite ends of a diameter and point A is on the circumference, then \BAC will always be 90±. Conversely, in 4ABC , if \BAC is
90± and a circle circumscribes 4ABC,
then side BC will always be the diameter.
�
- ▲TOP
- ページ: 6
- 4th Kyu Section 2
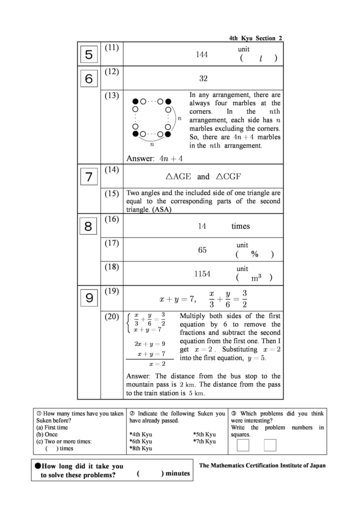
(11) (12) (13)
144
32
unit
(
l
)
In any arrangement, there are always four marbles at the corners. In the nth arrangement, each side has n marbles excluding the corners. So, there are 4n + 4 marbles in the nth arrangement.
Answer: 4n + 4 (14)
4AGE and 4CGF
equal to the corresponding parts of the second triangle. (ASA)
(15) Two angles and the included side of one triangle are (16) (17) (18) (19) (20)
14
65
times
unit
(
unit
%
m3
) )
1154
x + y = 7,
( x y 3 + = 3 6 2 x+y =7
2x + y = 9 x+y =7 x=2
(
x y 3 + = 3 6 2
Multiply both sides of the first equation by 6 to remove the fractions and subtract the second equation from the first one. Then I get x = 2 . Substituting x = 2 into the first equation, y = 5.
Answer: The distance from the bus stop to the mountain pass is 2 km. The distance from the pass to the train station is 5 km.
How many times have you taken Suken before? (a) First time (b) Once (c) Two or more times: ( ) times Indicate the following Suken you Which problems did you think have already passed. were interesting? Write the problem numbers in *4th Kyu *5th Kyu squares. *6th Kyu *7th Kyu *8th Kyu The Mathematics Certification Institute of Japan
●How long did it take you to solve these problems?
(
) minutes
�
- ▲TOP






